
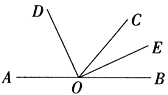
【题目】如图,O是直线AB上一点,OC是任意一条射线,OD,OE分别是∠AOC和∠BOC的平分线,
(1)图中∠BOD的补角是_______________;∠BOE的余角是____________________.
(2)如果∠BOE=![]() ∠AOD, 求∠BOE的度数。
∠AOD, 求∠BOE的度数。
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC为等边三角形,D为边BA延长线上一点,连接CD,以CD为一边作等边三角形CDE,连接AE.
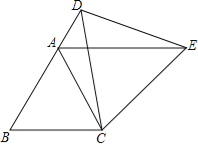
(1)求证:△CBD≌△CAE.
(2)判断AE与BC的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在实践中学习:
(1)如图1所示:已知AB∥CD,∠ABD=115°,根据 可得出:∠BDC的度数是 .
(2)如图2所示:已知AB∥CD,∠ABC=25°,∠EDC=40°,求∠BED的度数.
(3)如图3所示:已知MA∥NC,试确定∠A、∠B、∠C和∠E、∠F的关系,并说明理由.
(4)如图4所示:已知AB∥CD,∠ABE=α,∠FCD=β,∠CFE=γ,且BE⊥EF,试确定α、β、γ的关系,请说明理由.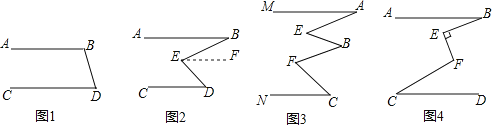
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOC=∠BOC,点P在OC上,PD⊥OA于点D,PE⊥OB于点E.若OD=8,OP=10,则PE的长为( ) 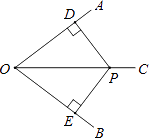
A.5
B.6
C.7
D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AE是△ABC的角平分线,AD⊥BC于点D,若∠BAC=128°,∠C=36°,则∠DAE的度数是( ) 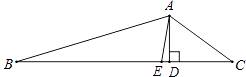
A.10°
B.12°
C.15°
D.18°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某校为搞好新校区的绿化,需要移植树木.该校九年级数学兴趣小组对某棵树木进行测量,此树木在移植时需要留出根部(即CD)1.3米.他们在距离树木5米的E点观测(即CE=5米),测量仪的高度EF=1.2米,测得树顶A的仰角∠BFA=40°,求此树的整体高度AD.(精确到0.1米)(参考数据:sin40°=0.6428,cos40°=0.7660,tan40°=0.8391)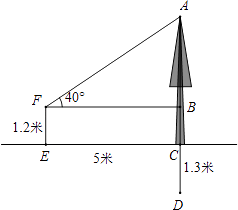
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某银行去年新增加居民存款10亿元人民币.
(1)经测量,100张面值为100元的新版人民币大约厚0.9厘米,如果将10亿元面值为100元的新版人民币摞起来,大约有多高?
(2)一台激光点钞机的点钞速度是8×104张/时,按每天点钞5小时计算,如果让点钞机点一遍10亿元面值为100元的新版人民币,点钞机大约要点多少天?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4),
(1)将△ABC各顶点的横坐标保持不变,纵坐标分别减5后得到△A1B1C1;
①请在图中画出△A1B1C1;
②求这个变换过程中线段AC所扫过的区域面积;
(2)将△ABC绕点(1,0)按逆时针方向旋转90°后得到的△A2B2C2,请在图中画出△A2B2C2,并分别写出△A2B2C2的顶点坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张阳从家里跑步去体育场,在那里锻炼了一会儿后,又走到文具店去买笔,然后走回家,如图是张阳离家的距离与时间的关系图象.
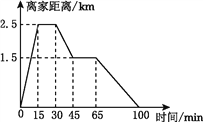
根据图象回答下列问题:
(1)体育场离张阳家多少千米?
(2)体育场离文具店多少千米?张阳在文具店逗留了多长时间?
(3)张阳从文具店到家的速度是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com