
【题目】如图,△ABC中,AB=AC,AM为BC边的中线,点D在边AC上,联结BD交AM于点F,延长BD至点E,使得![]() =
=![]() ,联结CE.
,联结CE.
求证:(1)∠ECD=2∠BAM;
(2)BF是DF和EF的比例中项.
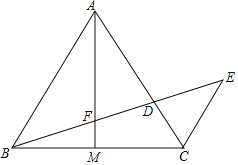
【答案】(1)详见解析;(2)详见解析.
【解析】
(1)由等腰三角形的性质可得∠BAC=2∠BAM,通过证明△ADB∽△CDE,可得∠BAC=∠ECD=2∠BAM;
(2)由等腰三角形的性质可得BF=CF,通过证明△DCF∽△CEF,可得![]() ,可得结论.
,可得结论.
证明:(1)∵AB=AC,AM为BC边的中线,
∴∠BAC=2∠BAM,
∵![]() =
=![]() ,∠ADB=∠CDE,
,∠ADB=∠CDE,
∴△ADB∽△CDE,
∴∠BAC=∠ECD,
∴∠ECD=2∠BAM;
(2)如图,连接CF,

∵AB=AC,AM为BC边的中线,
∴AM是BC的垂直平分线,
∴BF=CF,且AB=AC,AF=AF,
∵△ABF≌△ACF(SSS)
∴∠ABF=∠ACF,
由(1)可知:△ADB∽△CDE,
∴∠ABF=∠E,
∴∠ACF=∠E,且∠EFC=∠DFC,
∴△DCF∽△CEF,
∴![]() ,且BF=CF,
,且BF=CF,
∴BF2=DFEF,
∴BF是DF和EF的比例中项.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在一个不透明的布袋里装有![]() 个标号分别为
个标号分别为![]() 的小球,这些球除标号外无其它差别.从布袋里随机取出一个小球,记下标号为
的小球,这些球除标号外无其它差别.从布袋里随机取出一个小球,记下标号为![]() ,再从剩下的
,再从剩下的![]() 个小球中随机取出一个小球,记下标号为
个小球中随机取出一个小球,记下标号为![]() 记点
记点![]() 的坐标为
的坐标为![]() .
.
(1)请用画树形图或列表的方法写出点![]() 所有可能的坐标;
所有可能的坐标;
(2)求两次取出的小球标号之和大于![]() 的概率;
的概率;
(3)求点![]() 落在直线
落在直线![]() 上的概率.
上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=﹣![]() x+3的图象与反比例函数y=
x+3的图象与反比例函数y=![]() (x>0,k是常数)的图象交于A(a,2),B(4,b)两点.
(x>0,k是常数)的图象交于A(a,2),B(4,b)两点.
(1)求反比例函数的表达式;
(2)点C是第一象限内一点,连接AC,BC,使AC∥x轴,BC∥y轴,连接OA,OB.若点P在y轴上,且△OPA的面积与四边形OACB的面积相等,求点P的坐标.
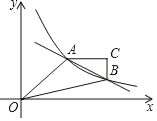
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,∠ABC和 ∠BAC的平分线交于点E,延长AE分别交BC, ⊙O于点F, D,连接BD.
(1)求证: BD=DE.
(2)若BD=6,AD=10,求EF的长.
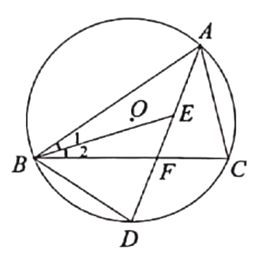
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)经过点A(-3,2),B(0,-2)其对称轴为直线x=![]() ,C(0,
,C(0, ![]() )为y轴上一点,直线AC与抛物线交于另一点D,
)为y轴上一点,直线AC与抛物线交于另一点D,

(1)求抛物线的解析式;
(2)在抛物线的对称轴上是否存在点F使△ADF是直角三角形,如果存在,求出点F的坐标,如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的边AB=20,面积为320,∠BAD<90°,⊙O与边AB,AD都相切,AO=10,则⊙O的半径长等于( )

A.5 B.6 C.2![]() D.3
D.3![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小芸设计的“过圆外一点作已知圆的切线”的尺规作图过程.
已知:⊙O及⊙O外一点P.
求作:⊙O的一条切线,使这条切线经过点P.
作法:①连接OP,作OP的垂直平分线l,交OP于点A;
②以A为圆心,AO为半径作圆,交⊙O于点M;
③作直线PM,则直线PM即为⊙O的切线.
根据小芸设计的尺规作图过程,
(1)用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成证明:
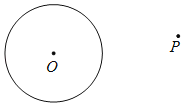
查看答案和解析>>
科目:初中数学 来源: 题型:
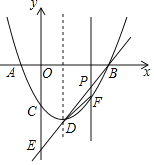
【题目】如图,对称轴为直线x=1的抛物线y=x2﹣bx+c与x轴交于A(x1,0)、B(x2,0)(x1<x2)两点,与y轴交于C点,且![]() +
+![]() =﹣
=﹣![]() .
.
(1)求抛物线的解析式;
(2)抛物线顶点为D,直线BD交y轴于E点;
①设点P为线段BD上一点(点P不与B、D两点重合),过点P作x轴的垂线与抛物线交于点F,求△BDF面积的最大值;
②在线段BD上是否存在点Q,使得∠BDC=∠QCE?若存在,求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com