
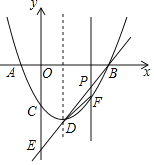
����Ŀ����ͼ���Գ���Ϊֱ��x=1��������y=x2��bx+c��x�ύ��A��x1��0����B��x2��0����x1��x2�����㣬��y�ύ��C�㣬��![]() +
+![]() =��
=��![]() ��
��
��1���������ߵĽ���ʽ��
��2�������߶���ΪD��ֱ��BD��y����E�㣻
�����PΪ�߶�BD��һ�㣨��P����B��D�����غϣ�������P��x��Ĵ����������߽��ڵ�F������BDF��������ֵ��
�����߶�BD���Ƿ���ڵ�Q��ʹ�á�BDC=��QCE�������ڣ������Q�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1�������߽���ʽΪ��y=x2��2x��3����2���ٵ�a=2ʱ��S���=��4+8��3=1���ڴ��ڵ�Q����Ϊ��![]() ����3��
����3��
����������1��Ӧ�öԳ��᷽�̡�����ϵ����ϵ��b��c
��2���������P�����ʾ��BDF����������ֵ��
�����ù��ɶ����涨����֤����BDC=90������QC��y�ᣬ����ɽ⣮
��1���������߶Գ���Ϊֱ��x=1
��-![]() ��1
��1
��b=2
��һԪ���η��̸���ϵ����ϵ��
x1+x2=-![]() ��x1x2=
��x1x2=![]() ��
��
��![]() ��
��
��![]() ��
��
��c=-3��
�������߽���ʽΪ��y=x2-2x-3��
��2���ɣ�1����D����Ϊ��1��-4����
��y=0ʱ��x2-2x-3=0��
���x1=-1��x2=3��
���B������3��0����
�����F������a��b����
���BDF�����S=![]() ����4-b����a-1��+
����4-b����a-1��+![]() ��-b����3-a��-
��-b����3-a��-![]() ��2��4��
��2��4��
������S=2a-b-6��
��b=a2-2a-3��
��S=2a-��a2-2a-3��-6=-a2+4a-3��
��a=-1��0��
�൱a=2ʱ��S���=-4+8-3=1��
�ڴ���.
����֪��D����Ϊ��1��-4������B����Ϊ��3��0����
��ֱ��BD����ʽΪ��y=2x-6��
���E������0��-6����
��BC��CD�����ɹ��ɶ����ã�
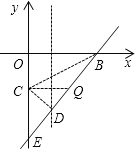
CB2=��3-0��2+��-3-0��2=18
CD2=12+��-4+3��2=2��
BD2=��-4��2+��3-1��2=20��
��CB2+CD2=BD2��
���BDC=90�㣬
�ߡ�BDC=��QCE��
���QCE=90�㣬
���Q������Ϊ-3��
����-3=2x-6��
��x=![]() ��
��
����ڵ�Q����Ϊ��![]() ��-3��
��-3��


 �����Ļ�������ҵϵ�д�
�����Ļ�������ҵϵ�д� ����������������ϵ�д�
����������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
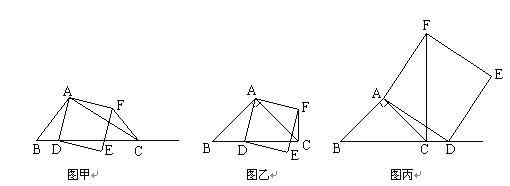
����Ŀ����ͼ�ף�����ABC�У���ACBΪ��ǣ���DΪ����BC��һ���㣬����AD����ADΪһ������AD���Ҳ���������ADEF��
����������⣺
��1�����AB=AC����BAC=90��
������D���߶�BC��ʱ�����B���غϣ�����ͼ�ң��߶�CF��BD֮���λ�ù�ϵΪ ��������ϵΪ ��
������D���߶�BC���ӳ�����ʱ����ͼ�������еĽ����Ƿ���Ȼ������Ϊʲô��
��2�����AB��AC����BAC��90����D���߶�BC���˶���
��̽��������ABC����һ��ʲô����ʱ��CF��BC����C��F�غϳ��⣩��������Ӧͼ�Σ���˵�����ɣ�����ͼ��д������
��3����AC��![]() ��BC=3���ڣ�2���������£���������ADEF�ı�DE���߶�CF�ཻ�ڵ�P�����߶�CP�������ֵ��
��BC=3���ڣ�2���������£���������ADEF�ı�DE���߶�CF�ཻ�ڵ�P�����߶�CP�������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
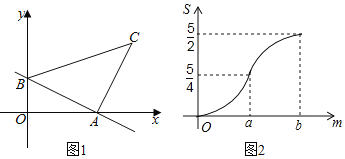
����Ŀ����ͼ1��ֱ��AB��x�ᡢy��ֱ��ཻ�ڵ�A��B�����߶�AB�Ƶ�A˳ʱ����ת90�����õ�AC������BC������ABC������BAƽ�ƣ�����C����x��ʱ�˶�ֹͣ����ƽ�ƾ���Ϊm��ƽ�ƺ��ͼ����x���·����ֵ����ΪS��S����m�ĺ���ͼ����ͼ2��ʾ������0��m��a��a��m��bʱ�������Ľ���ʽ��ͬ����
��1����գ���ABC�����Ϊ ��
��2����ֱ��AB�Ľ���ʽ��
��3����S����m�Ľ���ʽ����д��m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
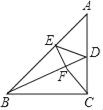
����Ŀ����ͼ����֪��Rt��ABC�У���ACB��90�㣬BD�ǡ�ABC�Ľ�ƽ���ߣ�E��AB��һ�㣬��AE��AD������ED����EF��BD��F������CF��������Ľ��ۣ�
��CD��CF��
�ڡ�EDF��45�㣻
�ۡ�BCF��45�㣻
����CD��4��AD��5����S��ADE��10��������ȷ���۵ĸ����ǣ�������
A. 1��B. 2��C. 3��D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��̽�����ɣ��۲�������ʽ��������⣮
1��3��4��22��
1��3��5��9��32��
1��3��5��7��16��42��
1��3��5��7��9��25��52��
��
(1)����룺1��3��5��7��9������19��________��
(2)����룺1��3��5��7��9������(2n��1)��________��
(3)�Լ��㣺101��103������197��199.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ʮһ���ƽ����ڼ䣬���ؾ���������֯�����л���������9��30�յ��ο�����Ϊ1���ˣ������������������ÿ��Ӵ����ο������仯���±���������ʾ��ǰһ����������������ʾ��ǰһ���ٵ���������
���� | 10��1�� | 10��2�� | 10��3�� | 10��4�� | 10��5�� | 10��6�� | 10��7�� |
�����仯 ����λ�����ˣ� |
|
|
|
|
|
|
|
��1������ݼ����ж��������ο��������������죬�ж������ˣ�
��2������9��30�յ��ο�����1����Ϊ����ÿ����Ʊ��Ϊ10Ԫ���ʻƽ����ڼ仴������ƽ��ÿ����Ʊ�����������Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ���ƺ����״Ϊ�ı���ABCD�����С�B��90�㣬AB��3m��BC��4m��CD��12m��AD��13m��������ƺ�������
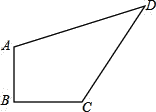
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����B��F��C��E��ֱ��l����F��C֮�䲻��ֱ�Ӳ���������A��D��l��࣬���AB=DE��AC=DF��BF=EC.

��1����֤����ABC�ա�DEF��
��2��ָ��ͼ������ƽ�е��߶Σ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ȱߡ�A1C1C2���ܳ�Ϊ1����C1D1��A1C2��D1����C1C2���ӳ�����ȡ��C3��ʹD1C3��D1C1������D1C3����C2C3Ϊ�����ȱߡ�A2C2C3����C2D2��A2C3��D2����C2C3���ӳ�����ȡ��C4��ʹD2C4��D2C2������D2C4����C3C4Ϊ�����ȱߡ�A3C3C4�����ҵ�A1��A2��A3��������ֱ��C1C2ͬ�࣬�����ȥ�����A1C1C2����A2C2C3����A3C3C4��������AnnCn+1���ܳ���Ϊ_____����n��2����nΪ������
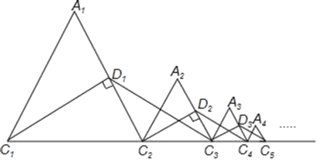
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com