
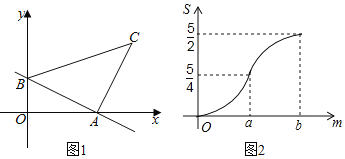
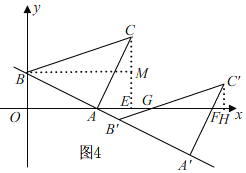
����Ŀ����ͼ1��ֱ��AB��x�ᡢy��ֱ��ཻ�ڵ�A��B�����߶�AB�Ƶ�A˳ʱ����ת90�����õ�AC������BC������ABC������BAƽ�ƣ�����C����x��ʱ�˶�ֹͣ����ƽ�ƾ���Ϊm��ƽ�ƺ��ͼ����x���·����ֵ����ΪS��S����m�ĺ���ͼ����ͼ2��ʾ������0��m��a��a��m��bʱ�������Ľ���ʽ��ͬ����
��1����գ���ABC�����Ϊ ��
��2����ֱ��AB�Ľ���ʽ��
��3����S����m�Ľ���ʽ����д��m��ȡֵ��Χ��
���𰸡���1��![]() ����2��ֱ��AB�Ľ���ʽΪy=��
����2��ֱ��AB�Ľ���ʽΪy=��![]() x+1����3��S=
x+1����3��S= ��
��
����������1����ͼ2���ƽ�Ƽ��ɵó����ۣ�
��2���жϳ���AOB�ա�CEA���ó�AE��OB��CE��OA������ͼ2֪����C���������ǵ�B�������2������������������ABC��������OB��OA�����ɵó����ۣ�
��3����������������������ε������ʽ�������ε������ɵó����ۣ�
��1�������ABC���ƶ���ͼ2֪����B�ƶ�����A��������ͼ2�У�m=aʱ��S=S��A'B'D=![]() ����C�ƶ���x����ʱ������m=bʱ��S=S��A'B'C'=S��ABC=
����C�ƶ���x����ʱ������m=bʱ��S=S��A'B'C'=S��ABC=![]() ��
��
�ʴ�Ϊ��![]() ��
��
��2����ͼ2������C��CE��x����E��
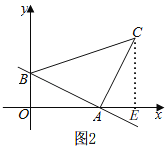
���AEC=��BOA=90�㣮
�ߡ�BAC=90�㣬
���OAB+��CAE=90�㣬
�ߡ�OAB+��OBA=90�㣬
���OBA=��CAE��
����ת֪��AB=AC��
����AOB�ա�CEA��
��AE=OB��CE=OA��
��ͼ2֪����C���������ǵ�B�������2����
��OA=2OB��
��AB2=5OB2��
�ɣ�1��֪��S��ABC=![]() =
=![]() AB2=
AB2=![]() ��5OB2��
��5OB2��
��OB=1��
��OA=2��
��A��2��0����B��0��1����
��ֱ��AB�Ľ���ʽΪy=��![]() x+1��
x+1��
��3���ɣ�2��֪��AB2=5��
��AB=![]() ��
��
�ٵ�0��m��![]() ʱ����ͼ3��
ʱ����ͼ3��
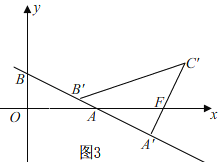
�ߡ�AOB=��AA'F����OAB=��A'AF��
����AOB�ס�AA'F��
��![]() ��
��
���˶�֪��AA'=m����![]() ��
��
��A'F=![]() m��
m��
��S=![]() AA'��A'F=
AA'��A'F=![]() m2��
m2��
�ڵ�![]() ��m��2
��m��2![]() ʱ����ͼ4��
ʱ����ͼ4��
ͬ�ٵķ����ã�A'F=![]() m��
m��
��C'F=![]() ��
��![]() m��
m��
����C��CE��x����E������B��BM��CE��E��
��BM=3��CM=1��
��֪����ACE�ס�FC'H��
��![]() ��
��
��![]() ��
��
��C'H=![]() ��
��
��Rt��FHC'��FH=![]() C'H=
C'H=![]() ��
��
��ƽ��֪����C'GF=��CBM��
�ߡ�BMC=��GHC'��
����BMC�ס�GHC'��
��![]() ��
��
��![]() ��
��
��GH=![]() ��
��
��GF=GH��FH=![]() ��
��
��S=S��A'B'C'��S��C'FG=![]() ��
��![]() ��
��![]() ��
��![]() =
=![]() ��
��![]() ��2
��2![]() ��m��2��
��m��2��
����S= ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ƽ��ֱ������ϵ�У���![]() ��
��![]() ���ϣ���
���ϣ���![]() ��
��![]() ��
��![]() ���ϣ�
���ϣ�![]() ��
��![]() ��
��![]() ����
����![]() ��������
��������![]() ��
��
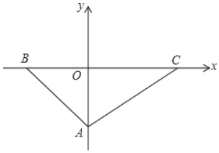
��1����![]() ��������
��������![]() ��
��![]() ��
��![]() �����ꣻ
�����ꣻ
��2������![]() ��
��![]() �����ú���ĸ
�����ú���ĸ![]() ��ʽ�ӱ�ʾ
��ʽ�ӱ�ʾ![]() �������
�������![]() ����
����
��3���ڣ�2���ʵ������£��Ƿ���ڵ�![]() ��ʹ
��ʹ![]() ���������
���������![]() �������������ڣ��������
�������������ڣ��������![]() �����ꣻ�������ڣ���˵�����ɣ�
�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���з��̣��飩��ʽ���飩��Ӧ���⣺
��1�����˽ӵ�240�������������1Сʱ����Ҫ��ǰ����������Һͼ�����������5Сʱ���.��֪��ÿСʱ��������4������ô�ס���ÿСʱ�������ٸ���
��2��ij����������![]() ��
��![]() ���ֻ�����20̨�������������������2̨
���ֻ�����20̨�������������������2̨![]() �ͻ�����1̨
�ͻ�����1̨![]() �ͻ����۸�Ϊ18��Ԫ��1̨
�ͻ����۸�Ϊ18��Ԫ��1̨![]() �ͻ�����2̨
�ͻ�����2̨![]() �ͻ����۸�Ϊ21��Ԫ.
�ͻ����۸�Ϊ21��Ԫ.
����һ̨![]() �ͻ�����һ̨
�ͻ�����һ̨![]() �ͻ����۸�ֱ��Ƕ�����Ԫ��
�ͻ����۸�ֱ��Ƕ�����Ԫ��
����֪1̨![]() �ͻ���ÿ�¿ɼӹ����400����1̨
�ͻ���ÿ�¿ɼӹ����400����1̨![]() �ͻ���ÿ�¿ɼӹ����800������Ԥ�㹺�����ֻ����ļ۸���140��Ԫ��ÿ�����ֻ����ӹ��������������12400������ô���ļ��ֹ��������ַ�����ʡǮ��
�ͻ���ÿ�¿ɼӹ����800������Ԥ�㹺�����ֻ����ļ۸���140��Ԫ��ÿ�����ֻ����ӹ��������������12400������ô���ļ��ֹ��������ַ�����ʡǮ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB��BC��AB=BC��DE��CD��DE=CD���밴��ͼ������ע�����ݣ�����ͼ��ʵ����Χ�ɵ�ͼ�ε����S�ǣ� ��

A. 36B. 48C. 72D. 108
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
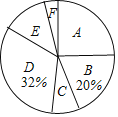
����Ŀ��ijУΪ�˽�ѧ����ϲ���������˶���������ѡȡ��У����ѧ�����е��飬Ҫ��ÿ��ѧ��ֻдһ����ϲ���������˶��������Ǹ��ݵ��������Ƶ�ͳ��ͼ����һ���֣�
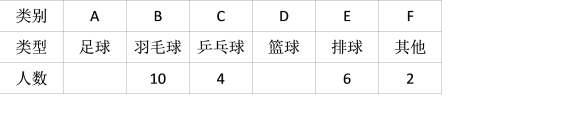
����������Ϣ������������⣺
��1���������ѧ���У���ϲ��ƹ������� �ˣ���ϲ�������ѧ����ռ�������������İٷֱ�Ϊ %��
��2��������ѧ��������Ϊ �ˣ����У���ϲ��������� �ˣ���ϲ�������ѧ����ռ�������������İٷֱ�Ϊ %��
��3����У����450��ѧ�������ݵ����������Ƹ�У��ϲ�������ѧ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڵȱ�������![]() ��
��![]() ��
��![]() ��
��![]() ���ϵ�һ�㣬��
���ϵ�һ�㣬��![]() ��
��![]() ���ϵ�һ�㣬����
���ϵ�һ�㣬����![]() ��
��![]() Ϊ�����ȱ�������
Ϊ�����ȱ�������![]() ����
����![]() ��
��
![]() ��ͼ1������
��ͼ1������![]() ���
���![]() �غ�ʱ��
�غ�ʱ��
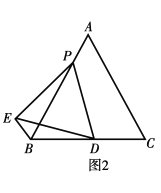
![]() �ҳ�ͼ�е�һ��ȫ�������Σ���֤����
�ҳ�ͼ�е�һ��ȫ�������Σ���֤����
![]() ��
��
![]() ��ͼ2����
��ͼ2����![]() �����
�����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
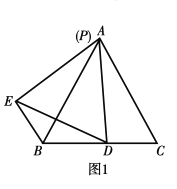
����Ŀ����ͼ����֪��OΪ��ABC��������ƽ���ߵĽ��㣬����O��OD��BC�ڵ�D����OD��4������ABC���ܳ���17�����ABC�����Ϊ��������

A. 34B. 17C. 8.5D. 4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
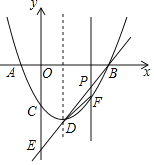
����Ŀ����ͼ���Գ���Ϊֱ��x=1��������y=x2��bx+c��x�ύ��A��x1��0����B��x2��0����x1��x2�����㣬��y�ύ��C�㣬��![]() +
+![]() =��
=��![]() ��
��
��1���������ߵĽ���ʽ��
��2�������߶���ΪD��ֱ��BD��y����E�㣻
�����PΪ�߶�BD��һ�㣨��P����B��D�����غϣ�������P��x��Ĵ����������߽��ڵ�F������BDF��������ֵ��
�����߶�BD���Ƿ���ڵ�Q��ʹ�á�BDC=��QCE�������ڣ������Q�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������и������������ڵ������������
��![]() ��+5����6.3��0����
��+5����6.3��0����![]() ��2
��2![]() ��6.9����7��210��0.031����43����10%
��6.9����7��210��0.031����43����10%
�������ϣ�{�� ����}
�������ϣ�{�� ����}
�Ǹ������ϣ�{�� ����}
���������ϣ�{�� ����}��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com