
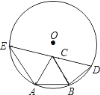
【题目】已知AB是半径为1的圆O的一条弦,且AB=a<1,以AB为一边在圆O内作正△ABC,点D为圆O上不同于点A的一点,且DB=AB=a,DC的延长线交圆O于点E,则AE的长为( )
A. ![]() B. 1 C.
B. 1 C. ![]() D. a
D. a
【答案】B
【解析】
试题此题可通过证△EAC≌△OAB,得AE=OA,从而求出EA的长;
△EAC和△OAB中,已知的条件只有AB=AC;由AB=BD,得![]() =
=![]() ,可得∠AED=∠AOB;
,可得∠AED=∠AOB;
四边形ABDE内角于⊙O,则∠EAB+∠D=180°,即∠EAC=180°﹣60°﹣∠D=120°﹣∠D;而∠ECA=180°﹣∠ACB﹣∠BCD=120°﹣∠BCD,上述两个式子中,由BD=AB=BC,易证得∠D=∠BCD,则∠ECA=∠EAC,即△EAC、△OAB都是等腰三角形,而两个等腰三角形的顶角相等,且底边AC=AB,易证得两个三角形全等,由此得解.
解:∵△ABC是等边三角形,
∴AB=BC=AC=BD=a,∠CAB=∠ACB=60°;
∵AB=BD,
∴![]() ,
,
∴∠AED=∠AOB;
∵BC=AB=BD,
∴∠D=∠BCD;
∵四边形EABD内接于⊙O,
∴∠EAB+∠D=180°,即∠EAC+60°+∠D=180°;
又∵∠ECA+60°+∠BCD=180°,
∴∠ECA=∠EAC,即△EAC是等腰三角形;
在等腰△EAC和等腰△OAB中,∠AEC=∠AOB,
∵AC=AB,
∴△EAC≌△OAB;
∴AE=OA=1.
故选B.


科目:初中数学 来源: 题型:
【题目】小明和小亮是一对双胞胎,他们的爸爸买了两套不同品牌的运动服送给他们,小明和小亮都想先挑选.于是小明设计了如下游戏来决定谁先挑选.游戏规则是:在一个不透明的袋子里装有除数字以外其它均相同的4个小球,上面分别标有数字1、2、3、4.一人先从袋中随机摸出一个小球,另一人再从袋中剩下的3个小球中随机摸出一个小球.若摸出的两个小球上的数字和为奇数,则小明先挑选;否则小亮先挑选.
(1)用树状图或列表法求出小明先挑选的概率;
(2)你认为这个游戏公平吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
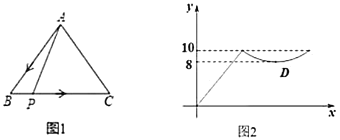
【题目】如图1,点![]() 从
从![]() 的顶点
的顶点![]() 出发,沿
出发,沿![]() 匀速运动,到点
匀速运动,到点![]() 停止运动.点
停止运动.点![]() 运动时,线段
运动时,线段![]() 的长度
的长度![]() 与运动时间
与运动时间![]() 的函数关系如图2所示,其中
的函数关系如图2所示,其中![]() 为曲线部分的最低点,则
为曲线部分的最低点,则![]() 的面积是________.
的面积是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
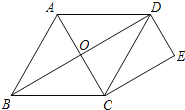
【题目】如图,菱形ABCD的对角线交于点O,点E是菱形外一点,DE∥AC,CE∥BD.
(1)求证:四边形DECO是矩形;
(2)连接AE交BD于点F,当∠ADB=30°,DE=2时,求AF的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,AD与⊙O相切于一点A,DE与⊙O相切于点E,点C为DE延长线上一点,且CE=CB.
⑴求证:BC为⊙O的切线;
⑵若AB=2![]() ,AD=2,求线段BC的长.
,AD=2,求线段BC的长.
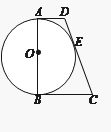
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一位运动员在距篮下4m处跳起投篮,球运行的路线是抛物线,当球运行的水平距离是2.5m时,达到最大高度3.5m,然后准确落入篮圈.已知篮圈中心到地面的距离为3.05m.
(1)建立如图所示的平面直角坐标系,求抛物线的解析式.
(2)该运动员身高1.8m,在这次跳投中,球在头顶上0.25m处出手,
问:球出手时,他距离地面的高度是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小婷在放学路上,看到隧道上方有一块宣传“中国﹣南亚博览会”的竖直标语牌CD.她在A点测得标语牌顶端D处的仰角为42°,测得隧道底端B处的俯角为30°(B,C,D在同一条直线上),AB=10m,隧道高6.5m(即BC=65m),求标语牌CD的长(结果保留小数点后一位).(参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90,![]() ≈1.73)
≈1.73)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com