
【题目】如图1,点![]() 从
从![]() 的顶点
的顶点![]() 出发,沿
出发,沿![]() 匀速运动,到点
匀速运动,到点![]() 停止运动.点
停止运动.点![]() 运动时,线段
运动时,线段![]() 的长度
的长度![]() 与运动时间
与运动时间![]() 的函数关系如图2所示,其中
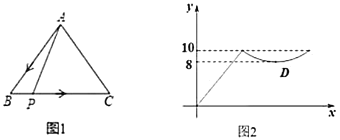
的函数关系如图2所示,其中![]() 为曲线部分的最低点,则
为曲线部分的最低点,则![]() 的面积是________.
的面积是________.
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案科目:初中数学 来源: 题型:
【题目】已知正比例函数和反比例函数的图象都经过点 A(3,3).
(1)求正比例函数和反比例函数的解析式;
(2)把直线 OA 向下平移后得到直线 l,与反比例函数的图象交于点 B(6,m),求 m 的值和直线 l 的解 析式;
(3)在(2)中的直线 l 与 x 轴、y 轴分别交于 C、D,求四边形 OABC 的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
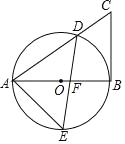
【题目】如图,AB是⊙O的直径,弦DE交AB于点F,⊙O的切线BC与AD的延长线交于点C,连接AE.
(1)试判断∠AED与∠C的数量关系,并说明理由;
(2)若AD=3,∠C=60°,点E是半圆AB的中点,则线段AE的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是边长为2,一个锐角等于60°的菱形纸片,小芳同学将一个三角形纸片的一个顶点与该菱形顶点D重合,按顺时针方向旋转三角形纸片,使它的两边分别交CB、BA(或它们的延长线)于点E、F,∠EDF=60°,当CE=AF时,如图1小芳同学得出的结论是DE=DF.
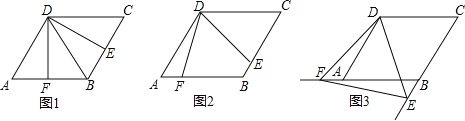
(1)继续旋转三角形纸片,当CE≠AF时,如图2小芳的结论是否成立?若成立,加以证明;若不成立,请说明理由;
(2)再次旋转三角形纸片,当点E、F分别在CB、BA的延长线上时,如图3请直接写出DE与DF的数量关系;
(3)连EF,若△DEF的面积为y,CE=x,求y与x的关系式,并指出当x为何值时,y有最小值,最小值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
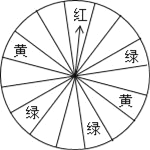
【题目】“六一”儿童节期间,某商厦为了吸引顾客,设立了一个可以自由转动的转盘(转盘被平均分成16份),并规定:顾客每购买100元的商品,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准哪个区域,顾客就可以获得相应的奖品.
颜色 | 奖品 |
红色 | 玩具熊 |
黄色 | 童话书 |
绿色 | 彩笔 |
小明和妈妈购买了125元的商品,请你分析计算:
(1)小明获得奖品的概率是多少?
(2)小明获得童话书的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
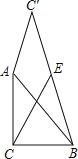
【题目】如图,已知△ABC中,∠ACB=90°,AC=BC=2,将直角边AC绕A点逆时针旋转至AC′,连接BC′,E为BC′的中点,连接CE,则CE的最大值为( ).
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的材料并解答问题:
例:解方程x4﹣5x2+4=0,这是一个一元四次方程,根据该方程的特点,它的解法通常是:
设x2=y,那么x4=y2,于是原方程可变为y2﹣5y+4=0,
解得y1=1,y2=4.
当y=1时,x2=1,∴x=±1;
当y=4时,x2=4,∴x=±2;
∴原方程有四个根:x1=1,x2=﹣1,x3=2,x4=﹣2.
仿照上例解方程:(x2﹣2x)2+(x2﹣2x)﹣6=0
查看答案和解析>>
科目:初中数学 来源: 题型:
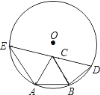
【题目】已知AB是半径为1的圆O的一条弦,且AB=a<1,以AB为一边在圆O内作正△ABC,点D为圆O上不同于点A的一点,且DB=AB=a,DC的延长线交圆O于点E,则AE的长为( )
A. ![]() B. 1 C.
B. 1 C. ![]() D. a
D. a
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们在解决数学问题时,经常采用“转化”(或“化归”)的思想方法,即把待解决的问题,通过转化归结到一类已解决或比较容易解决的问题.
譬如,求解一元二次方程,通常把它转化为两个一元一次方程来解;求解分式方程,通常把它转化为整式方程来解,只是因为分式方程“去分母”时可能产生增根,所以解分式方程必须检验.
请你运用上述把“未知”转化为“已知”的数学思想,解决下列问题.
(1)解方程:x3+x2﹣2x=0;
(2)解方程:![]() =x;
=x;
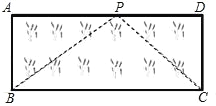
(3)如图,已知矩形草坪 ABCD 的长 AD=8m,宽 AB=3m,小华把一根长为10m 的绳子的一端固定在点 B,沿草坪边沿 BA、AD 走到点 P 处,把长绳 PB 段拉直并固定在点 P,然后沿草坪边沿 PD、DC 走到点 C 处,把长绳剩下的一段拉直,长绳的另一端恰好落在点 C.求 AP 的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com