
【题目】我们在解决数学问题时,经常采用“转化”(或“化归”)的思想方法,即把待解决的问题,通过转化归结到一类已解决或比较容易解决的问题.
譬如,求解一元二次方程,通常把它转化为两个一元一次方程来解;求解分式方程,通常把它转化为整式方程来解,只是因为分式方程“去分母”时可能产生增根,所以解分式方程必须检验.
请你运用上述把“未知”转化为“已知”的数学思想,解决下列问题.
(1)解方程:x3+x2﹣2x=0;
(2)解方程:![]() =x;
=x;
(3)如图,已知矩形草坪 ABCD 的长 AD=8m,宽 AB=3m,小华把一根长为10m 的绳子的一端固定在点 B,沿草坪边沿 BA、AD 走到点 P 处,把长绳 PB 段拉直并固定在点 P,然后沿草坪边沿 PD、DC 走到点 C 处,把长绳剩下的一段拉直,长绳的另一端恰好落在点 C.求 AP 的长.
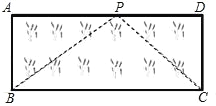
【答案】(1)x1=0,x2=﹣2,x3=1;(2)x=3;(3)AP 的长为 4m.
【解析】
(1)因式分解多项式,然后得结论;
(2)两边平方,把无理方程转化为整式方程,求解,注意验根;
(3)设AP的长为xm,根据勾股定理和BP+CP=10,可列出方程,由于方程含有根号,两边平方,把无理方程转化为整式方程,求解即可.
(1)x3+x2-2x=0,
x(x2+x-2)=0,
x(x+2)(x-1)=0
所以x=0或x+2=0或x-1=0
∴x1=0,x2=-2,x3=1;
(2)![]() =x,
=x,
方程的两边平方,得2x+3=x2
即x2-2x-3=0
(x-3)(x+1)=0
∴x-3=0或x+1=0
∴x1=3,x2=-1,
当x=-1时,![]() =
=![]() =1≠-1,
=1≠-1,
所以-1不是原方程的解.
所以方程![]() =x的解是x=3;
=x的解是x=3;
(3)因为四边形ABCD是矩形,
所以∠A=∠D=90°,AB=CD=3m,
设AP=xm,则PD=(8-x)m,
因为BP+CP=10,
BP=![]() ,CP=
,CP=![]() ,
,
∴![]() =10,
=10,
∴![]() ,
,
两边平方,得(8-x)2+9=100-20![]() +9+x2
+9+x2
整理,得5![]() =4x+9
=4x+9
两边平方并整理,得x2-8x+16=0
即(x-4)2=0
所以x=4.
经检验,x=4是方程的解.
答:AP的长为4m.


科目:初中数学 来源: 题型:
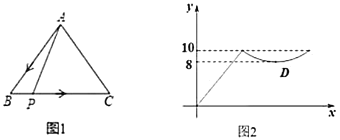
【题目】如图1,点![]() 从
从![]() 的顶点
的顶点![]() 出发,沿
出发,沿![]() 匀速运动,到点
匀速运动,到点![]() 停止运动.点
停止运动.点![]() 运动时,线段
运动时,线段![]() 的长度
的长度![]() 与运动时间
与运动时间![]() 的函数关系如图2所示,其中
的函数关系如图2所示,其中![]() 为曲线部分的最低点,则
为曲线部分的最低点,则![]() 的面积是________.
的面积是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一位运动员在距篮下4m处跳起投篮,球运行的路线是抛物线,当球运行的水平距离是2.5m时,达到最大高度3.5m,然后准确落入篮圈.已知篮圈中心到地面的距离为3.05m.
(1)建立如图所示的平面直角坐标系,求抛物线的解析式.
(2)该运动员身高1.8m,在这次跳投中,球在头顶上0.25m处出手,
问:球出手时,他距离地面的高度是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小婷在放学路上,看到隧道上方有一块宣传“中国﹣南亚博览会”的竖直标语牌CD.她在A点测得标语牌顶端D处的仰角为42°,测得隧道底端B处的俯角为30°(B,C,D在同一条直线上),AB=10m,隧道高6.5m(即BC=65m),求标语牌CD的长(结果保留小数点后一位).(参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90,![]() ≈1.73)
≈1.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分9分)如图,以⊿ABC的一边AB为直径的半圆与其它两边AC,BC的交点分别为D,E,且![]() .
.
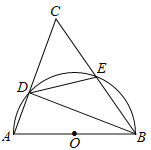
(1)试判断⊿ABC的形状,并说明理由;
(2)已知半圆的半径为5,BC=12,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
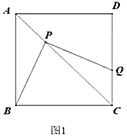
【题目】操作:将一把三角尺放在边长为1的正方形![]() 上,并使它的直角顶点
上,并使它的直角顶点![]() 在对角线
在对角线![]() 上滑动,直角的一边始终经过点
上滑动,直角的一边始终经过点![]() ,另一边与射线
,另一边与射线![]() 相交于点
相交于点![]() .
.
探究:设![]() ,
,![]() 两点间的距离为
两点间的距离为![]() .
.
(1)点![]() 在
在![]() 边上时,线段
边上时,线段![]() 与线段
与线段![]() 之间有怎样的大小关系?试证明你观察得到的结论(如图1);
之间有怎样的大小关系?试证明你观察得到的结论(如图1);
(2)点![]() 在边
在边![]() 上时设四边形
上时设四边形![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 之间的函数解析式,并写出自变量的取值范围(如图2);
之间的函数解析式,并写出自变量的取值范围(如图2);
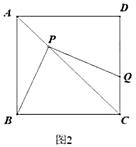
(3)点![]() 在线段
在线段![]() 上滑动时,
上滑动时,![]() 是否可能成为等腰三角形?如果可能,指出所有能使
是否可能成为等腰三角形?如果可能,指出所有能使![]() 成为等腰三角形的点
成为等腰三角形的点![]() 的位置,并直接写出相应的
的位置,并直接写出相应的![]() 的值;如果不可能,试说明理由(如图3).(图4、图5、图6的形状、大小相同,图4供操作、实验用,图5和图6备用).
的值;如果不可能,试说明理由(如图3).(图4、图5、图6的形状、大小相同,图4供操作、实验用,图5和图6备用).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个盒子里有完全相同的三个小球,球上分别标上数字-1、1、2.随机摸出一个小球(不放回),其数字记为p,再随机摸出另一个小球,其数字记为q,则p,q使关于x的方程x2+px+q=0有实数根的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的布袋里装有3个球,其中2个红球,1个白球,它们除颜色外其余都相同.
(1)求摸出1个球是白球的概率;
(2)摸出1个球,记下颜色后放回,并搅均,再摸出1个球.求两次摸出的球恰好颜色不同的概率(要求画树状图或列表);
(3)现再将n个白球放入布袋,搅均后,使摸出1个球是白球的概率为![]() .求n的值.
.求n的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com