
【题目】如图,已知抛物线y=x2﹣2bx﹣3(b为常数,b<0).
发现:(1)抛物线y=x2﹣2bx﹣3总经过一定点,定点坐标为 ;
(2)抛物线的对称轴为直线x= (用含b的代数式表示),位于y轴的 侧.
思考:若点P(﹣2,﹣1)在抛物线y=x2﹣2bx﹣3上,抛物线与反比例函数y=![]() (k>0,x>0)的图象在第一象限内交点的横坐标为a,且满足2<a<3,试确定k的取值范围.
(k>0,x>0)的图象在第一象限内交点的横坐标为a,且满足2<a<3,试确定k的取值范围.
探究:设点A是抛物线上一点,且点A的横坐标为m,以点A为顶点做边长为1的正方形ABCD,AB⊥x轴,点C在点A的右下方,若抛物线与CD边相交于点P(不与D点重合且不在y轴上),点P的纵坐标为﹣3,求b与m之间的函数关系式.
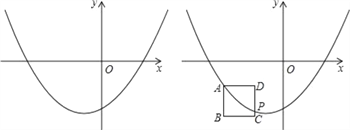
【答案】发现:(1) (0,﹣3);(2)b,左;思考:10<k<36;探究:b=![]() .
.
【解析】试题分析:解:(1)抛物线与y轴的交点为定点;当x=0时,y=x2﹣2bx﹣3=﹣3,
所以抛物线经过定点(0,﹣3);
(2)利用抛物线的对称轴方程得到抛物线的对称轴为直线x=b,然后利用b的范围确定抛物线的对称轴在y轴的左侧;
思考:把P点坐标代入y=x2﹣2bx﹣3得b=﹣1,则抛物线解析式为y=x2+2x﹣3,再分别计算出a=2和a=3所对应的二次函数值,从而确定反比例函数与抛物线的交点的位置,然后利用反比例函数图象上点的坐标特征确定k的范围;
探究:设A(m,m2+2m﹣3),利用正方形的性质得D(m+1,m2+2m﹣3),则P点的坐标为(m+1,﹣3),然后把P(m+1,﹣3)代入y=x2﹣2bx﹣3可得到b与m的关系式.
试题解析:解:(1)当x=0时,y=x2﹣2bx﹣3=﹣3,
所以抛物线经过定点(0,﹣3);
(2)抛物线的对称轴为直线x=﹣![]() =b,
=b,
因为b<0,
所以抛物线的对称轴在y轴的左侧;
故答案为(0,﹣3),b,左;
思考:把P(﹣2,﹣1)代入y=x2﹣2bx﹣3得4+4b﹣3=﹣1,解得b=﹣1,
抛物线解析式为y=x2+2x﹣3,
当a=2时,y=x2+2x﹣3=4+4﹣3=5,
当a=3时,y=x2+2x﹣3=9+6﹣3=12,
所以二次函数图象与反比例函数的交点在抛物线上的点(2,5),(3,12)之间,
所以2×5<k<3×12,
即10<k<36;
探究:设A(m,m2+2m﹣3),
∵正方形ABCD的边长为1,AB⊥x轴,
∴D(m+1,m2+2m﹣3),
∴P点的坐标为(m+1,﹣3),
把P(m+1,﹣3)代入y=x2﹣2bx﹣3得(m+1)2﹣2b(m+1)﹣3=﹣3,
而m+1≠0,
∴m+1﹣2b=0,
∴b=![]() .
.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:
【题目】动物园中有熊猫,孔雀,大象,梅花鹿四种可爱动物,为了解本班同学喜欢哪种动物的人最多,则调查的对象是( ).
A.本班的每一个同学
B.熊猫,孔雀,大象,梅花鹿
C.同学们的选票
D.记录下来的数据
查看答案和解析>>
科目:初中数学 来源: 题型:
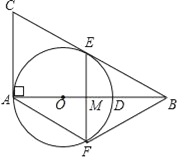
【题目】如图,在Rt△ABC中,∠BAC=90°,O是AB边上的一点,以OA为半径的⊙O与边BC相切于点E.
(1)若AC=6,BC=10,求⊙O的半径.
(2)过点E作弦EF⊥AB于M,连接AF,若∠AFE=2∠ABC,求证:四边形ACEF是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小林家、小华家与图书馆依次在一条直线上.小林、小华两人同时各自从家沿直线匀速步行到图书馆借阅图书,已知小林到达图书馆花了20分钟.设两人出发x(分钟)后,小林离小华家的距离为y(米),y与x的函数关系如图所示.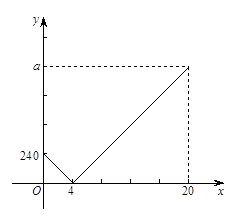
(1)小林的速度为米/分钟,a= , 小林家离图书馆的距离为米;
(2)已知小华的步行速度是40米/分钟,设小华步行时与家的距离为y1(米),请在图中画出y1(米)与x(分钟 )的函数图象;
(3)小华出发几分钟后两人在途中相遇?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】体育委员统计了全班同学60秒跳绳的次数,并列出下列人数次数分布表,回答下列问题:
次数x | 人数 |
60≤x<80 | 2 |
80≤x<100 | 5 |
100≤x<120 | 21 |
120≤x<140 | 13 |
140≤x<160 | 8 |
160≤x<180 | 4 |
(1)全班有多少人?
(2)组距、组数是多少?
(3)跳绳次数在100≤x<140范围内同学有多少人,占全班的百分之几(精确到0.01%)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明家准备装修一套新住房,若甲、乙两个装饰公司,合做需6周完成,需工钱5.2万元;若甲公司单独做4周后,剩下的由乙公司来做,还需9周才能完成,需工钱4.8万元,若只选一个公司单独完成,从节约开支角度考虑,小明家是选甲公司、还是乙公司请你说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com