
【题目】如图,已知抛物线![]() (
(![]() )与x轴交于点A(1,0)和点B(﹣3,0),与y轴交于点C,且OC=OB.
)与x轴交于点A(1,0)和点B(﹣3,0),与y轴交于点C,且OC=OB.
(1)求此抛物线的解析式;
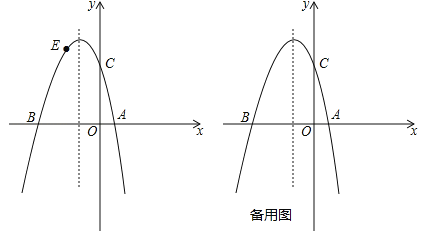
(2)若点E为第二象限抛物线上一动点,连接BE,CE,求四边形BOCE面积的最大值,并求出此时点E的坐标;
(3)点P在抛物线的对称轴上,若线段PA绕点P逆时针旋转90°后,点A的对应点A′恰好也落在此抛物线上,求点P的坐标.
【答案】(1)![]() ;(2)当a=
;(2)当a=![]() 时,S四边形BOCE最大,且最大值为
时,S四边形BOCE最大,且最大值为![]() ,此时,点E坐标为(
,此时,点E坐标为(![]() ,
,![]() );(3)P(﹣1,1)或(﹣1,﹣2).
);(3)P(﹣1,1)或(﹣1,﹣2).
【解析】
试题分析:(1)将A、B两点的坐标代入抛物线的解析式中,即可求出二次函数的解析式;
(2)过E作EF⊥x轴于F.设E(a,![]() )(﹣3<a<0),则EF=
)(﹣3<a<0),则EF=![]() ,BF=a+3,OF=﹣a,∴S四边形BOCE=
,BF=a+3,OF=﹣a,∴S四边形BOCE=![]() =
=![]() BFEF+
BFEF+![]() (OC+EF)OF =
(OC+EF)OF =![]() ,配方即可得出结论,当a=
,配方即可得出结论,当a=![]() 时,
时,![]() =
=![]() 大,即可得到点E的坐标;
大,即可得到点E的坐标;
(3)由P在抛物线的对称轴上,设出P坐标为(﹣2,m),如图所示,过A′作A′N⊥对称轴于N,由旋转的性质可证明△A′NP≌△PMA,得到A′N=PM=|m|,PN=AM=2,表示出A′坐标,将A′坐标代入抛物线解析式中求出相应m的值,即可确定出P的坐标.
试题解析:(1)∵抛物线![]() (
(![]() )与x轴交于点A(1,0)和点B(﹣3,0),∴OB=3,∵OC=OB,∴OC=3,∴c=3,∴
)与x轴交于点A(1,0)和点B(﹣3,0),∴OB=3,∵OC=OB,∴OC=3,∴c=3,∴![]() ,解得:
,解得:![]() ,∴所求抛物线解析式为:
,∴所求抛物线解析式为:![]() ;
;
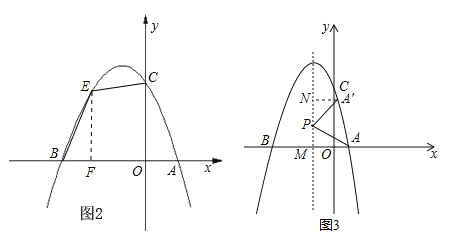
(2)如图2,过点E作EF⊥x轴于点F,设E(a,![]() )(﹣3<a<0),∴EF=
)(﹣3<a<0),∴EF=![]() ,BF=a+3,OF=﹣a,∴S四边形BOCE=
,BF=a+3,OF=﹣a,∴S四边形BOCE=![]() =
=![]() BFEF+
BFEF+![]() (OC+EF)OF=
(OC+EF)OF=![]() =
=![]() =
=![]() ,∴当a=
,∴当a=![]() 时,S四边形BOCE最大,且最大值为
时,S四边形BOCE最大,且最大值为![]() .此时,点E坐标为(
.此时,点E坐标为(![]() ,
,![]() );
);
(3)∵抛物线![]() 的对称轴为x=﹣1,点P在抛物线的对称轴上,∴设P(﹣1,m),∵线段PA绕点P逆时针旋转90°后,点A的对应点A′恰好也落在此抛物线上,如图,∴PA=PA′,∠APA′=90°,如图3,过A′作A′N⊥对称轴于N,设对称轴于x轴交于点M,∴∠NPA′+∠MPA=∠NA′P+∠NPA′=90°,∴∠NA′P=∠NPA,在△A′NP与△APM中,∵∠A′NP=∠AMP=90°,∠NA′P=∠MPA,PA′=AP,∴△A′NP≌△PMA,∴A′N=PM=|m|,PN=AM=2,∴A′(m﹣1,m+2),代入
的对称轴为x=﹣1,点P在抛物线的对称轴上,∴设P(﹣1,m),∵线段PA绕点P逆时针旋转90°后,点A的对应点A′恰好也落在此抛物线上,如图,∴PA=PA′,∠APA′=90°,如图3,过A′作A′N⊥对称轴于N,设对称轴于x轴交于点M,∴∠NPA′+∠MPA=∠NA′P+∠NPA′=90°,∴∠NA′P=∠NPA,在△A′NP与△APM中,∵∠A′NP=∠AMP=90°,∠NA′P=∠MPA,PA′=AP,∴△A′NP≌△PMA,∴A′N=PM=|m|,PN=AM=2,∴A′(m﹣1,m+2),代入![]() 得:
得:![]() ,解得:m=1,m=﹣2,∴P(﹣1,1),(﹣1,﹣2).
,解得:m=1,m=﹣2,∴P(﹣1,1),(﹣1,﹣2).


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】如图,点D,E分别在线段AB,AC上,CD与BE相交于O点,已知AB=AC,现添加以下的哪个条件仍不能判定△ABE≌△ACD( ) 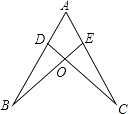
A.∠B=∠C
B.AD=AE
C.BD=CE
D.BE=CD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在基地参加社会实践话动中,带队老师考问学生:基地计划新建一个矩形的生物园地,一边靠旧墙(墙足够长),另外三边用总长69米的不锈钢栅栏围成,与墙平行的一边留一个宽为3米的出入口,如图所示,如何设计才能使园地的而积最大?下面是两位学生争议的情境:

请根据上面的信息,解决问题:
(1)设AB=x米(x>0),试用含x的代数式表示BC的长;
(2)请你判断谁的说法正确,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把矩形纸片ABCD纸沿对角线折叠,设重叠部分为△EBD,那么下列说法错误的是( ) 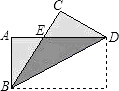
A.△EBD是等腰三角形,EB=ED
B.折叠后∠ABE和∠CBD一定相等
C.折叠后得到的图形是轴对称图形
D.△EBA和△EDC一定是全等三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过第2011次运动后,动点P的坐标是 . 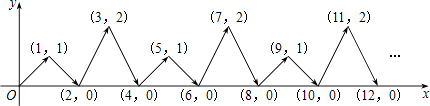
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com