
����Ŀ����ͼ����ABCD��,AB=12,BC=8,E��F�ֱ�ΪAB��CD���е�,��P��Q��A. Cͬʱ����,�ڱ�AD��CB����ÿ��1����λ��D��B�˶�,�˶�ʱ��Ϊt(0<t<8).
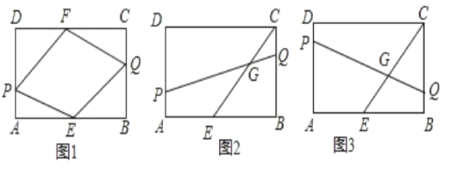
(1)��ͼ1������PE��EQ��QF��PF����֤������t��0<t<8��ȡ�κ�ֵ���ı���PEQF��Ϊƽ���ı��Σ�
(2)��ͼ2������PQ��CE��G����PG=4QG����t��ֵ��
(3)���˶������У��Ƿ����ijʱ��ʹ��PQ��CE��G?�����ڣ������t��ֵ���������ڣ���˵������
���𰸡���1������������2��![]() ����3�������ڣ����ɼ�����.
����3�������ڣ����ɼ�����.
��������
��1���ɾ��ε����ʵó�CD=AB=12��AD=BC=8����A=��B=��C=��D=90������SAS֤����APE�ա�CQF���ó�PE=QF��ͬ����PF=QE�����ɵó����ۣ�
��2����������ã�AP=CQ=t����PD=QB=8-t����EF��BC��CD��E����PQ��H��֤��EH������ABQP����λ�ߣ���������λ�߶����ó�EH=![]() ��AP+BQ��=4��֤��GH��GQ=3��2����ƽ���ߵó���EGH�ס�CGQ���ó���Ӧ�߳ɱ���
��AP+BQ��=4��֤��GH��GQ=3��2����ƽ���ߵó���EGH�ס�CGQ���ó���Ӧ�߳ɱ���![]() �����ɵó�t��ֵ��
�����ɵó�t��ֵ��
��3���ɹ��ɶ������CE=![]() =10����EM��BC��PQ��M���ɣ�2���ã�ME=4��֤����GCQ�ס�BCE���ó���Ӧ�߳ɱ������CG=t
=10����EM��BC��PQ��M���ɣ�2���ã�ME=4��֤����GCQ�ס�BCE���ó���Ӧ�߳ɱ������CG=t![]() ���ó�EG=10-
���ó�EG=10-![]() t����ƽ����֤����GME�ס�GQC���ó���Ӧ�߳ɱ��������t=0��t=8.5�����ɵó����ۣ�
t����ƽ����֤����GME�ס�GQC���ó���Ӧ�߳ɱ��������t=0��t=8.5�����ɵó����ۣ�
(1)֤�������ı���ABCD�Ǿ��Σ�
��CD=AB=12,AD=BC=8,��A=��B=��C=��D=90����
��E��F�ֱ�ΪAB��CD���е㣬
��AE=BE=6��DF=CF=6��
��AE=BE=DF=CF��
�ߵ�P��Q��A. Cͬʱ�������ڱ�AD��CB����ÿ��1����λ��D��B�˶���
��AP=CQ=t��
�ڡ�APE�͡�CQF��,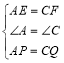 ��
��
���APE�ա�CQF(SAS),
��PE=QF��
ͬ����PF=QE��
���ı���PEQF��Ϊƽ���ı��Σ�
(2)��������ã�AP=CQ=t��
��PD=QB=8t��
��EF��BC��CD��E����PQ��H����ͼ2��ʾ��
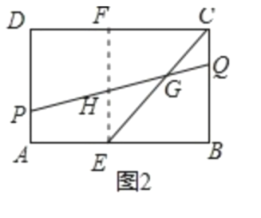
��FΪCD���е㣬HΪPQ���е㣬EF=BC=8��
��EH������ABQP����λ�ߣ�
��EH=![]() (AP+BQ)=4��
(AP+BQ)=4��
��PG=4QG��
��GH:GQ=3:2��
��EF��BC��
���EGH�ס�CGQ��
��![]() =
=![]() ,��4t=
,��4t=![]() ��
��
��ã�t=![]() ��
��
����PG=4QG,t��Ϊ![]() ֵ;
ֵ;
(3)�����ڣ��������£�
�ߡ�B=90����BE=6��BC=8��
��CE=![]() =10��
=10��
��EM��BC��PQ��M����ͼ3��ʾ��
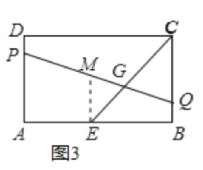
��(2)�ã�ME=4��
��PQ��CE��
���CGQ=90��=��B��
�ߡ�GCQ=��BCE��
���GCQ�ס�BCE��
��![]() ,��
,��![]() =
=![]() ��
��
��CG=![]() t��
t��
��EG=10![]() t��
t��
��EM��BC��
���GME�ס�GQC��
��![]() ,��
,��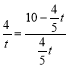 ��
��
��ã�t=0��t=8.5��
��0<t<8��
����ڡ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�κ���y=��kx+k�뷴��������y=��![]() ��k��0����ͬһ����ϵ�е�ͼ������ǣ�������
��k��0����ͬһ����ϵ�е�ͼ������ǣ�������
A.  B.
B. 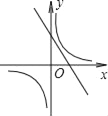 C.
C.  D.
D. 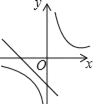
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���C=90������ACΪֱ������O����AB��D������O��OE��AB����BC��E��
��1����֤��EDΪ��O�����ߣ�
��2�������O�İ뾶Ϊ![]() ��ED=2���ӳ�EO����O��F������DF��AF������ADF�������
��ED=2���ӳ�EO����O��F������DF��AF������ADF�������

���𰸡���1��֤������������2��![]()
�������������������1����������OD����OE��AB������ƽ��������������ε����ʣ���֤��![]() ��
��![]() ���ɵ�
���ɵ�![]() �����֤��
�����֤��![]() Ϊ
Ϊ![]() �����ߣ�
�����ߣ�
��2������CD������ֱ�����Ե�Բ�ܽ���ֱ�ǣ����ɵ�![]() ���ù��ɶ����������
���ù��ɶ����������![]() �ij�������OE��AB��֤��
�ij�������OE��AB��֤��![]() �������������εĶ�Ӧ�߳ɱ������������
�������������εĶ�Ӧ�߳ɱ������������![]() �ij���Ȼ���������Ǻ�����֪ʶ�����
�ij���Ȼ���������Ǻ�����֪ʶ�����![]() ��
��![]() �ij���Ȼ������S��ADF=S����ABEF-S����DBEF��ô𰸣�
�ij���Ȼ������S��ADF=S����ABEF-S����DBEF��ô𰸣�
���������(1)֤��������OD��

��OE��AB��
���COE=��CAD����EOD=��ODA��
��OA=OD,
���OAD=��ODA��
���COE=��DOE��
�ڡ�COE�͡�DOE�У�
 ���COE�ա�DOE(SAS)��
���COE�ա�DOE(SAS)��
![]()
��ED��OD��
��ED��![]() �����ߣ�
�����ߣ�
(2)����CD����OE��M��
��Rt��ODE��
��OD=32��DE=2��
![]()
��OE��AB��
���COE�ס�CAB��
![]() ��AB=5��
��AB=5��
��AC��ֱ����
![]()
![]()
![]()
![]()
��EF��AB��
![]()
![]()
![]()
��S��ADF=S����ABEFS����DBEF
![]()
���ADF�����Ϊ![]()

�����͡������
��������
25
����Ŀ������Ŀ����֪��������y=ax2+ax+b��a��0����ֱ��y=2x+m��һ��������M��1��0������a��b��
��1����b��a�Ĺ�ϵʽ�������ߵĶ���D���꣨��a�Ĵ���ʽ��ʾ����
��2��ֱ���������ߵ�����һ�������ΪN������DMN�������a�Ĺ�ϵʽ��
��3��a=��1ʱ��ֱ��y=��2x���������ڵڶ������ڵ�G����G��H����ԭ��Գƣ��ֽ��߶�GH��y������ƽ��t����λ��t��0�������߶�GH����������������ͬ�Ĺ����㣬����t��ȡֵ��Χ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ,һ�κ���y=kx+3��ͼ���뷴��������y=![]() (x>0)��ͼ���ڵ�P.PA��x���ڵ�A,PB��y���ڵ�B. һ�κ�����ͼ��ֱ�x�ᡢy���ڵ�C. ��D,��S��DBP=27,
(x>0)��ͼ���ڵ�P.PA��x���ڵ�A,PB��y���ڵ�B. һ�κ�����ͼ��ֱ�x�ᡢy���ڵ�C. ��D,��S��DBP=27,![]()
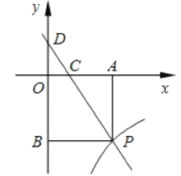
(1)���D�����ꣻ
(2)��һ�κ����뷴���������Ľ���ʽ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
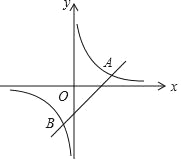
����Ŀ����ͼ����֪һ�κ���y=x��2�뷴��������y=![]() ��ͼ����A��B���㣮
��ͼ����A��B���㣮
��1����A��B��������ꣻ
��2���۲�ͼ��ֱ��д��һ�κ���ֵС�ڷ���������ֵ��x��ȡֵ��Χ��
��3������ԭ��ΪO������AOB�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������У��Ǽ��������( )
A. ��![]() ����һ����������жԽ��ߣ����������ηֳ�
����һ����������жԽ��ߣ����������ηֳ�![]() ��������
��������
B. �������У����������������ȵĵ��������ߴ�ֱƽ���ߵĽ���
C. �����ε����߽������ηֳ������ȵ�������
D. һ��Ա�ƽ����һ��Ա���ȵ��ı�����ƽ���ı���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�DZ߳�Ϊ1�������Σ�E��FΪBD����ֱ���ϵ����㣮��AE=![]() ����EAF=135���������½�����ȷ���ǣ�������
����EAF=135���������½�����ȷ���ǣ�������
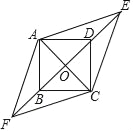
A. DE=1 B. tan��AFO=![]() C. AF=
C. AF=![]() D. �ı���AFCE�����Ϊ
D. �ı���AFCE�����Ϊ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����a�ķ���![]() �Ľ�Ҳ�ǹ���x�ķ���
�Ľ�Ҳ�ǹ���x�ķ���![]() =11�Ľ�.
=11�Ľ�.
(1)��a��b��ֵ��
(2)���߶�AB=a����ֱ��AB��ȡһ��P��ǡ��ʹ![]() ����QΪAP���е㣬���߶�BQ�ij�.
����QΪAP���е㣬���߶�BQ�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����O����ABC��һ�㣬����OB��OC������AB��OB��OC��AC���е�D��E��F��G�������ᣬ�õ��ı���DEFG��
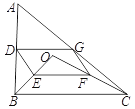
��![]() ����֤���ı���DEFG��ƽ���ı��Σ�
����֤���ı���DEFG��ƽ���ı��Σ�
��![]() �����
�����![]() ��
�� ![]() ��
�� ![]() ����
����![]() �ij���
�ij���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com