
【题目】已知:如图,一次函数y=kx+3的图象与反比例函数y=![]() (x>0)的图象交于点P.PA⊥x轴于点A,PB⊥y轴于点B. 一次函数的图象分别交x轴、y轴于点C. 点D,且S△DBP=27,
(x>0)的图象交于点P.PA⊥x轴于点A,PB⊥y轴于点B. 一次函数的图象分别交x轴、y轴于点C. 点D,且S△DBP=27,![]()
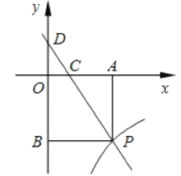
(1)求点D的坐标;
(2)求一次函数与反比例函数的解析式
【答案】(1)(0,3);(2)y=![]() x+3,y=
x+3,y=![]()
【解析】
(1)根据一次函数与y轴的交点,从而得出D点的坐标.
(2)根据在Rt△COD和Rt△CAP中,![]() ,OD=3,再根据S△DBP=27,从而得
,OD=3,再根据S△DBP=27,从而得
(1)∵一次函数y=kx+3与y轴相交,
∴令x=0,解得y=3,得D的坐标为(0,3);
(2)∵OD⊥OA,AP⊥OA,
∠DCO=∠ACP,
∠DOC=∠CAP=90°,
∴Rt△COD∽Rt△CAP,则![]() ,OD=3,
,OD=3,
∴AP=OB=6,
∴DB=OD+OB=9,
在Rt△DBP中,∴![]() =27,
=27,
即![]() ,
,
∴BP=6,故P(6,6),
把P坐标代入y=kx+3,得到k=![]() ,
,
则一次函数的解析式为:y=![]() x+3;
x+3;
把P坐标代入反比例函数解析式得m=36,
则反比例解析式为:y=![]() ;
;


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:初中数学 来源: 题型:
【题目】如图①,已知线段AB=12cm,点C为线段AB上的一动点,点D,E分别是AC和BC中点.
(1)若点C恰好是AB的中点,则DE=_______cm;
(2)若AC=4cm,求DE的长;
(3)试说明无论AC取何值(不超过12cm),DE的长不变;
(4)如图②,已知∠AOB=120°,过角的内部任一点C画射线OC.若OD,OE分别平分∠AOC和∠BOC.试说明∠DOE的度数与射线OC的位置无关.
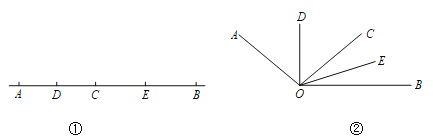
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(探索新知)
如图1,点C在线段AB上,图中共有3条线段:AB、AC和BC,若其中有一条线段的长度是另一条线段长度的两倍,则称点C是线段AB的“二倍点”.
(1)一条线段的中点 这条线段的“二倍点”;(填“是”或“不是”)
(深入研究)
如图2,若线段AB=20cm,点M从点B的位置开始,以每秒2cm的速度向点A运动,当点M到达点A时停止运动,运动的时间为t秒.
(2)问t为何值时,点M是线段AB的“二倍点”;
(3)同时点N从点A的位置开始,以每秒1cm的速度向点B运动,并与点M同时停止.请直接写出点M是线段AN的“二倍点”时t的值.
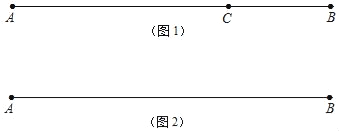
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为丰富学生课余生活,我校准备开设兴趣课堂.为了了解学生对绘画、书法、舞蹈、乐器这四个兴趣小组的喜爱情况,在全校进行随机抽样调查,并根据收集的数据绘制了下面两幅统计图(信息尚不完整),请根据图中提供的信息,解答下面的问题:

(1)此次共调查了多少名同学?
(2)将条形图补充完整,并计算扇形统计图中乐器部分的圆心角的度数;
(3)如果我校共有1000名学生参加这4个课外兴趣小组,而每个教师最多只能辅导本组的25名学生,估计书法兴趣小组至少需要准备多少名教师?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为2的正方形ABCD中,点P是边AD上的动点(点P不与点A、点D重合),点Q是边CD上一点,联结PB、PQ,且∠PBC=∠BPQ.
(1)当QD=QC时,求∠ABP的正切值;
(2)设AP=x,CQ=y,求y关于x的函数解析式;
(3)联结BQ,在△PBQ中是否存在度数不变的角?若存在,指出这个角,并求出它的度数;若不存在,请说明理由.
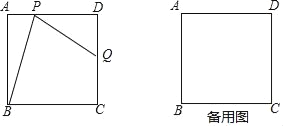
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)阅读下面材料:
点A、B在数轴上分别表示实数a、b,A、B两点之间的距离表示为|AB|.当A、B两点中有一点在原点时,不妨设点A在原点,如图1,|AB|=|OB|=|b|=|a﹣b|;当A、B两点都不在原点时,
①如图2,点A、B都在原点的右边|AB|=|OB|﹣|OA|=|b|﹣|a|=b﹣a=|a﹣b|;
②如图3,点A、B都在原点的左边,|AB|=|OB|﹣|OA|=|b|﹣|a|=﹣b﹣(﹣a)=|a﹣b|;
③如图4,点A、B在原点的两边,|AB|=|OB|+|OA|=|a|+|b|=a+(﹣b)=|a﹣b|

(2)回答下列问题:
①数轴上表示2和5的两点之间的距离是 ,数轴上表示﹣2和﹣5的两点之间的距离是 ,数轴上表示1和﹣3的两点之间的距离是 ;
②数轴上表示x和﹣1的两点A和B之间的距离是 ,如果|AB|=2,那么x为 ;
③代数式|x+1|+|x﹣2|取最小值时,相应的整数x的取值是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图矩形ABCD中,AB=12,BC=8,E、F分别为AB、CD的中点,点P、Q从A. C同时出发,在边AD、CB上以每秒1个单位向D、B运动,运动时间为t(0<t<8).
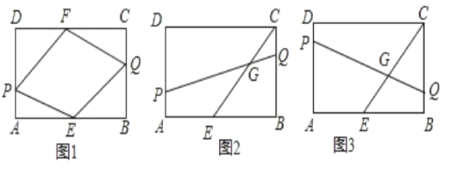
(1)如图1,连接PE、EQ、QF、PF,求证:无论t在0<t<8内取任何值,四边形PEQF总为平行四边形;
(2)如图2,连接PQ交CE于G,若PG=4QG,求t的值;
(3)在运动过程中,是否存在某时刻使得PQ⊥CE于G?若存在,请求出t的值:若不存在,请说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长方形ABCD中,点M为CD中点,将△MBC沿BM翻折至△MBE,若∠AME = α,∠ABE = β,则 α 与 β 之间的数量关系为( )
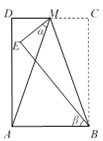
A. α+3β=180° B. β-α=20° C. α+β=80° D. 3β-2α=90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①是一块瓷砖的图案,用这种瓷砖来铺设地面,如果铺成一个2×2的正方形图案(如图②),其中完整的圆共有5个,如果铺成一个3×3的正方形图案(如图③),其中完整的圆共有13个,如果铺成一个4×4的正方形图案(如图④),其中完整的圆共有25个,若这样铺成一个10×10的正方形图案,则其中完整的圆共有( )个.
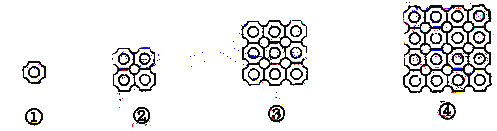
A.145 B.146 C.180 D.181
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com