
【题目】如图,在长方形ABCD中,点M为CD中点,将△MBC沿BM翻折至△MBE,若∠AME = α,∠ABE = β,则 α 与 β 之间的数量关系为( )
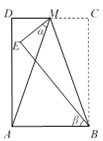
A. α+3β=180° B. β-α=20° C. α+β=80° D. 3β-2α=90°
【答案】D
【解析】
直接利用平行线的性质结合翻折变换的性质得出△ADM≌△BCM(SAS),进而利用直角三角形的性质得出答案.
∵M为CD中点,
∴DM=CM,
在△ADM和△BCM中
∵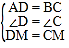 ,
,
∴△ADM≌△BCM(SAS),
∴∠AMD=∠BMC,AM=BM
∴∠MAB=∠MBA
∵将点C绕着BM翻折到点E处,
∴∠EBM=∠CBM,∠BME=∠BMC=∠AMD
∴∠DME=∠AMB
∴∠EBM=∠CBM=![]() (90°-β)
(90°-β)
∴∠MBA=![]() (90°-β)+ β=
(90°-β)+ β=![]() (90°+β)
(90°+β)
∴∠MAB=∠MBA=![]() (90°+β)
(90°+β)
∴∠DME=∠AMB=180°-∠MAB-∠MBA=90°-β
∵长方形ABCD中,
∴CD∥AB
∴∠DMA=∠MAB=![]() (90°+β)
(90°+β)
∴∠DME+∠AME=∠ABE+∠MBE
∵∠AME=α,∠ABE=β,
∴90°-β+α=β+![]() (90°-β)
(90°-β)
∴3β-2α=90°
故选:D.


科目:初中数学 来源: 题型:
【题目】张师傅在铺瓷砖时发现,用8块大小一样的小长方形瓷砖恰好可以拼成一个大的长方形,如图①.然后,他用这8块瓷砖又拼出一个正方形,如图②,中间恰好空出一个边长为1的小正方形(阴影部分).
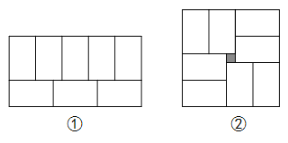
(1)请你根据图①写出小长方形的长与宽之比为 ;
(2)请你根据图②列出方程,求出小长方形的长与宽.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,一次函数y=kx+3的图象与反比例函数y=![]() (x>0)的图象交于点P.PA⊥x轴于点A,PB⊥y轴于点B. 一次函数的图象分别交x轴、y轴于点C. 点D,且S△DBP=27,
(x>0)的图象交于点P.PA⊥x轴于点A,PB⊥y轴于点B. 一次函数的图象分别交x轴、y轴于点C. 点D,且S△DBP=27,![]()
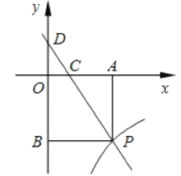
(1)求点D的坐标;
(2)求一次函数与反比例函数的解析式
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,是假命题的是( )
A. 过![]() 边形一个顶点的所有对角线,将这个多边形分成
边形一个顶点的所有对角线,将这个多边形分成![]() 个三角形
个三角形
B. 三角形中,到三个顶点距离相等的点是三条边垂直平分线的交点
C. 三角形的中线将三角形分成面积相等的两部分
D. 一组对边平行另一组对边相等的四边形是平行四边形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是边长为1的正方形,E,F为BD所在直线上的两点.若AE=![]() ,∠EAF=135°,则以下结论正确的是( )
,∠EAF=135°,则以下结论正确的是( )
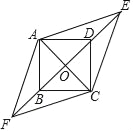
A. DE=1 B. tan∠AFO=![]() C. AF=
C. AF=![]() D. 四边形AFCE的面积为
D. 四边形AFCE的面积为![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了加强学生的安全意识,组织学生参加安全知识竞赛,并从中抽取了部分学生的成绩(得分均为整数,满分100分)进行统计,绘制了两幅尚不完整的统计图如图所示,
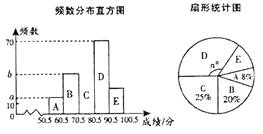
根据统计图中的信息解答下列问题:
(1)若![]() 组的频数比
组的频数比![]() 组小
组小![]() ,则频数分布直方图中
,则频数分布直方图中![]() ________,
________,![]() ________;
________;
(2)扇形统计图中![]() ________,并补全频数分布直方图;
________,并补全频数分布直方图;
(3)若成绩在![]() 分以上为优秀,全校共有
分以上为优秀,全校共有![]() 名学生,请估计成绩优秀的学生有多少名?
名学生,请估计成绩优秀的学生有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于a的方程![]() 的解也是关于x的方程
的解也是关于x的方程![]() =11的解.
=11的解.
(1)求a、b的值;
(2)若线段AB=a,在直线AB上取一点P,恰好使![]() ,点Q为AP的中点,求线段BQ的长.
,点Q为AP的中点,求线段BQ的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某村耕地总面积为50公顷,且该村人均耕地面积y(单位:公顷/人)与总人口x(单位:人)的函数图象如图所示,则下列说法正确的是( )
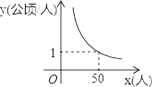
A. 该村人均耕地面积随总人口的增多而增多
B. 该村人均耕地面积y与总人口x成正比例
C. 若该村人均耕地面积为2公顷,则总人口有100人
D. 当该村总人口为50人时,人均耕地面积为1公顷
查看答案和解析>>
科目:初中数学 来源: 题型:
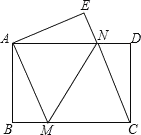
【题目】如图,将一张矩形纸片ABCD沿直线MN折叠,使点C落在点A处,点D落在点E处,直线MN交BC于点M,交AD于点N.
(1)求证:CM=CN;
(2)若△CMN的面积与△CDN的面积比为3:1,ND=1.
①求MC的长.
②求MN的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com