
【题目】已知关于a的方程![]() 的解也是关于x的方程
的解也是关于x的方程![]() =11的解.
=11的解.
(1)求a、b的值;
(2)若线段AB=a,在直线AB上取一点P,恰好使![]() ,点Q为AP的中点,求线段BQ的长.
,点Q为AP的中点,求线段BQ的长.
【答案】(1)a=10,b=3;(2)![]() 或
或![]() .
.
【解析】
(1)根据方程同解,求出第一个方程的解,可求出第二个方程中的b;
(2)分类讨论,①点P在线段AB上,根据![]() ,可求出PB的长,根据Q是线段PB的中点,可求出BQ的长;②点P在线段AB的延长线上,根据
,可求出PB的长,根据Q是线段PB的中点,可求出BQ的长;②点P在线段AB的延长线上,根据![]() ,可求出PB的长,根据Q是线段PB的中点,可得BQ的长.
,可求出PB的长,根据Q是线段PB的中点,可得BQ的长.
解:![]()
![]()
![]()
![]()
∵x=a=10,
把x=10代入![]() 得:
得:![]() ,解得:b=3;
,解得:b=3;
(2)①当点P在线段AB上时,如图所示:
![]()
∴AB=a=10,![]() ,
,
∴AP=3PB,则AB=AP+PB=4PB=10,
∴PB=2.5,
∵Q是线段PB的中点,
∴![]() ;
;
②当点P在线段AB延长线上时,如图所示:
![]()
∴AB=a=10,![]() ,
,
∴AP=3PB,AB=AP-PB=2PB=10,
∴PB=5,
∵Q是线段PB的中点,
∴![]() ,
,
综上所述:BQ的长为![]() 或
或![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】(探索新知)
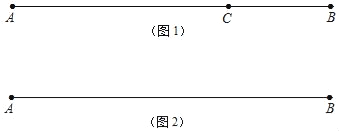
如图1,点C在线段AB上,图中共有3条线段:AB、AC和BC,若其中有一条线段的长度是另一条线段长度的两倍,则称点C是线段AB的“二倍点”.
(1)一条线段的中点 这条线段的“二倍点”;(填“是”或“不是”)
(深入研究)
如图2,若线段AB=20cm,点M从点B的位置开始,以每秒2cm的速度向点A运动,当点M到达点A时停止运动,运动的时间为t秒.
(2)问t为何值时,点M是线段AB的“二倍点”;
(3)同时点N从点A的位置开始,以每秒1cm的速度向点B运动,并与点M同时停止.请直接写出点M是线段AN的“二倍点”时t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图矩形ABCD中,AB=12,BC=8,E、F分别为AB、CD的中点,点P、Q从A. C同时出发,在边AD、CB上以每秒1个单位向D、B运动,运动时间为t(0<t<8).
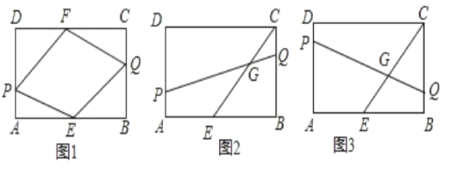
(1)如图1,连接PE、EQ、QF、PF,求证:无论t在0<t<8内取任何值,四边形PEQF总为平行四边形;
(2)如图2,连接PQ交CE于G,若PG=4QG,求t的值;
(3)在运动过程中,是否存在某时刻使得PQ⊥CE于G?若存在,请求出t的值:若不存在,请说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长方形ABCD中,点M为CD中点,将△MBC沿BM翻折至△MBE,若∠AME = α,∠ABE = β,则 α 与 β 之间的数量关系为( )
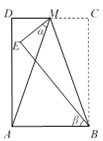
A. α+3β=180° B. β-α=20° C. α+β=80° D. 3β-2α=90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:有三个角相等的四边形叫做三等角四边形.
(1)在三等角四边形![]() 中,
中,![]() ,则
,则![]() 的取值范围为________.
的取值范围为________.
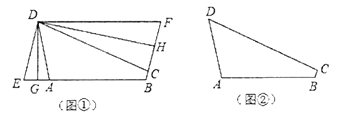
(2)如图①,折叠平行四边形![]() ,使得顶点
,使得顶点![]() 、
、![]() 分别落在边
分别落在边![]() 、
、![]() 上的点
上的点![]() 、
、![]() 处,折痕为
处,折痕为![]() 、
、![]() .求证:四边形
.求证:四边形![]() 为三等角四边形;
为三等角四边形;
(3)如图②,三等角四边形![]() 中,
中,![]() ,若
,若![]() ,
,![]() ,
,![]() ,则
,则![]() 的长度为多少?
的长度为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,线段AB和CD数轴上运动,A开始时与原点重合,且![]() .
.
(1)若AB=10,且B为线段AC的中点,求线段AD的长.
(2)在(1)的条件下,线段AB和CD同时开始向右运动,线段AB的速度为5个单位/秒,线段CD的速度为3个单位/秒,经过t秒恰好有![]() ,求t的值.
,求t的值.
(3)若线段AB和CD同时开始向左运动,且线段AB的速度大于线段CD的速度,在点A和C之间有一点P(不与点B重合),且有![]() ,此时线段BP为定值吗?若是请求出这个定值,若不是请说明理由.
,此时线段BP为定值吗?若是请求出这个定值,若不是请说明理由.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=3,BC=4,O为矩形ABCD的中心,以D为圆心1为半径作⊙D,P为⊙D上的一个动点,连接AP、OP,则△AOP面积的最大值为( )
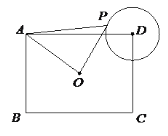
A. 4 B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①是一块瓷砖的图案,用这种瓷砖来铺设地面,如果铺成一个2×2的正方形图案(如图②),其中完整的圆共有5个,如果铺成一个3×3的正方形图案(如图③),其中完整的圆共有13个,如果铺成一个4×4的正方形图案(如图④),其中完整的圆共有25个,若这样铺成一个10×10的正方形图案,则其中完整的圆共有( )个.
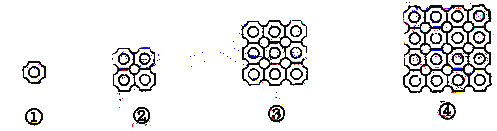
A.145 B.146 C.180 D.181
查看答案和解析>>
科目:初中数学 来源: 题型:
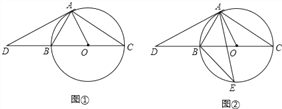
【题目】已知BC是⊙O的直径,AD是⊙O的切线,切点为A,AD交CB的延长线于点D,连接AB,AO.
(1)如图①,求证:∠OAC=∠DAB;
(2)如图②,AD=AC,若E是⊙O上一点,求∠E的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com