
【题目】定义:有三个角相等的四边形叫做三等角四边形.
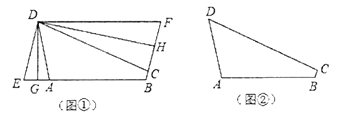
(1)在三等角四边形![]() 中,
中,![]() ,则
,则![]() 的取值范围为________.
的取值范围为________.
(2)如图①,折叠平行四边形![]() ,使得顶点
,使得顶点![]() 、
、![]() 分别落在边
分别落在边![]() 、
、![]() 上的点
上的点![]() 、
、![]() 处,折痕为
处,折痕为![]() 、
、![]() .求证:四边形
.求证:四边形![]() 为三等角四边形;
为三等角四边形;
(3)如图②,三等角四边形![]() 中,
中,![]() ,若
,若![]() ,
,![]() ,
,![]() ,则
,则![]() 的长度为多少?
的长度为多少?
【答案】(1)![]() ;(2)见解析;(3)
;(2)见解析;(3)![]() 的长度为
的长度为![]() .
.
【解析】
(1)根据四边形的内角和是360°,确定出∠BAD的范围;
(2)由四边形DEBF为平行四边形,得到∠E=∠F,且∠E+∠EBF=180°,再根据等角的补角相等,判断出∠DAB=∠DCB=∠ABC即可;
(3)延长BA,过D点作DG⊥BA,继续延长BA,使得AG=EG,连接DE;延长BC,过D点作DH⊥BC,继续延长BC,使得CH=HF,连接DF,由SAS证明△DEG≌△DAG,得出AD=DE=![]() ,∠DAG=∠DEA,由SAS证明△DFH≌△DCH,得出CD=DF=6,∠DCH=∠DFH,证出DE∥BF,BE∥DF,得出四边形DEBF是平行四边形,得出DF=BE=6,DE=BF=
,∠DAG=∠DEA,由SAS证明△DFH≌△DCH,得出CD=DF=6,∠DCH=∠DFH,证出DE∥BF,BE∥DF,得出四边形DEBF是平行四边形,得出DF=BE=6,DE=BF=![]() ,由等腰三角形的性质得出EG=AG=
,由等腰三角形的性质得出EG=AG=![]() (BE-AB)=1,在Rt△DGA中,由勾股定理求出DG=
(BE-AB)=1,在Rt△DGA中,由勾股定理求出DG=![]() =4,由平行四边形DEBF的面积求出
=4,由平行四边形DEBF的面积求出![]() ,在Rt△DCH中,由勾股定理求出
,在Rt△DCH中,由勾股定理求出![]() ,即可得出BC的长度.
,即可得出BC的长度.
(1)∵![]()
∴![]()
∴![]()
∵![]()
∴![]()
∴![]()
故答案为:![]()
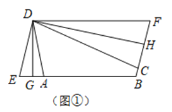
(2)证明:∵四边形![]() 为平行四边形,
为平行四边形,
∴![]() ,
,![]()
∴![]()
∵![]() ,
,![]()
∴![]()
∵![]() ,
,![]() ,
,![]()
∴![]()
∴四边形![]() 是三等角四边形;
是三等角四边形;
(3)延长![]() ,过
,过![]() 点作
点作![]() ,继续延长
,继续延长![]() ,使得
,使得![]() ,连接
,连接![]() ;延长
;延长![]() ,过
,过![]() 点作
点作![]() ,继续延长
,继续延长![]() ,使得
,使得![]() ,连接
,连接![]() ,如图所示:
,如图所示:
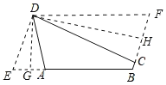
在![]() 和
和![]() 中,
中,
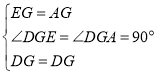
∴![]()
![]() ,
,
∴![]() ,
,![]()
同理可得![]() ,
,![]()
∴![]() ,
,![]()
∵![]()
∴![]() ,
,![]()
∴![]() ,
,![]()
∴四边形![]() 是平行四边形,
是平行四边形,
∴![]() ,
,![]() ,
,
∴![]()
在![]() 中,
中,![]()
∵平行四边形![]() 的面积
的面积![]() ,
,
即:![]()
∴![]()
在![]() 中,
中,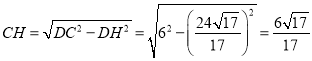
∴![]()
故答案为:![]() 的长度为
的长度为![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,以△ABC的三边为边在BC同侧分别作等边三角形,即△ABD,△BCE,△ACF.
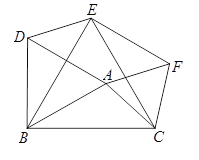
(1)四边形ADEF为__________四边形;
(2)当△ABC满足条件____________时,四边形ADEF为矩形;
(3)当△ABC满足条件____________时,四边形ADEF为菱形;
(4)当△ABC满足条件____________时,四边形ADEF不存在.
查看答案和解析>>
科目:初中数学 来源: 题型:
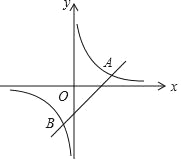
【题目】如图,已知一次函数y=x﹣2与反比例函数y=![]() 的图象交于A、B两点.
的图象交于A、B两点.
(1)求A、B两点的坐标;
(2)观察图象,直接写出一次函数值小于反比例函数值的x的取值范围;
(3)坐标原点为O,求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是边长为1的正方形,E,F为BD所在直线上的两点.若AE=![]() ,∠EAF=135°,则以下结论正确的是( )
,∠EAF=135°,则以下结论正确的是( )
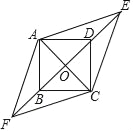
A. DE=1 B. tan∠AFO=![]() C. AF=
C. AF=![]() D. 四边形AFCE的面积为
D. 四边形AFCE的面积为![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 在 数轴上对应的数分别用
在 数轴上对应的数分别用![]() 表示,且
表示,且![]() .
.![]() 是数轴的一动点.
是数轴的一动点.
⑴在数轴上标出![]() 的位置,并求出
的位置,并求出![]() 之间的距离;
之间的距离;
⑵数轴上一点![]() 距
距![]() 点24个单位的长度,其对应的数
点24个单位的长度,其对应的数![]() 满足
满足![]() ,当
,当![]() 点满足
点满足![]() 时,求
时,求![]() 点对应的数.
点对应的数.
⑶动点![]() 从原点开始第一次向左移动1个单位,第二次向右移动3个单位长度,第三次向左移动5个单位长度,第四次向右移动7个单位长度,……点
从原点开始第一次向左移动1个单位,第二次向右移动3个单位长度,第三次向左移动5个单位长度,第四次向右移动7个单位长度,……点![]() 能移动到与
能移动到与![]() 或
或![]() 重合的位置吗?若能,请探究第几次移动时重合;若不能,请说明理由.
重合的位置吗?若能,请探究第几次移动时重合;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于a的方程![]() 的解也是关于x的方程
的解也是关于x的方程![]() =11的解.
=11的解.
(1)求a、b的值;
(2)若线段AB=a,在直线AB上取一点P,恰好使![]() ,点Q为AP的中点,求线段BQ的长.
,点Q为AP的中点,求线段BQ的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学七年级开展演讲比赛,学校决定购买一些笔记本和钢笔作为奖品.现了解情况如下:甲、乙两家商店出售两种同样品牌的笔记本和钢笔.笔记本定价为每本20元,钢笔每支定价5元,经洽谈后,甲店每买一本笔记本赠一支钢笔;乙店全部按定价的9折优惠.七年级需笔记本20本,钢笔若干支(不小于20支).问:
(1)如果购买钢笔![]() (
(![]() 不小于20)支,则在甲店购买需付款 ______ 元,在乙店购买需付款 _______________ 元.(用x的代数式表示)
不小于20)支,则在甲店购买需付款 ______ 元,在乙店购买需付款 _______________ 元.(用x的代数式表示)
(2)当购买钢笔多少支时,在两店购买付款一样?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用同样规格的黑白两种颜色的正方形瓷砖,按下图的方式铺地板:

(1)观察图形,填写下表:
图形 | (1) | (2) | (3) | …… |
黑色瓷砖的块数 | 4 | …… | ||
黑白两种瓷砖的总块数 | 15 | …… |
(2)依上推测,第n个图形中黑色瓷砖的块数为__________________;黑白两种瓷砖的总块数为__________________(都用含n的代数式表示)
(3)白色瓷砖的块数可能比黑色瓷砖的块数多2014块吗?若能,求出是第几个图形;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】年是我市“创建国家卫生城市”第一年,为了了解本班![]() 名学生对“创卫”的知晓率,某同学采取随机抽样的方法进行问卷调查,调查分为四个选项:
名学生对“创卫”的知晓率,某同学采取随机抽样的方法进行问卷调查,调查分为四个选项:![]() 非常了解,
非常了解,![]() 比较了解,
比较了解,![]() 基本了解,
基本了解,![]() 不甚了解.数据整理如下:
不甚了解.数据整理如下:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
请画出条形图和扇形图来描述以上统计数据.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com