
【题目】如图,以△ABC的三边为边在BC同侧分别作等边三角形,即△ABD,△BCE,△ACF.
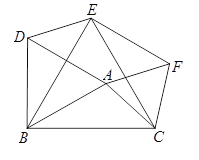
(1)四边形ADEF为__________四边形;
(2)当△ABC满足条件____________时,四边形ADEF为矩形;
(3)当△ABC满足条件____________时,四边形ADEF为菱形;
(4)当△ABC满足条件____________时,四边形ADEF不存在.
【答案】(1)平行;(2)∠BAC=150°;(3)AB=AC且∠BAC≠60°;(4)∠BAC=60°.
【解析】
(1)可先证明△ABC≌△DBE,可得DE=AC,又有AC=AF,可得DE=AF,同理可得AD=EF,根据两组对边分别相等的四边形是平行四边形,可证四边形ADEF是平行四边形;
(2)如四边形ADEF是矩形,则∠DAF=90°,又有∠BAD=∠FAC=60°,可得∠BAC=150°,故∠BAC=150°时,四边形ADEF是矩形;
(3)利用菱形的性质与判定得出即可;
(4)根据∠BAC=60°时,∠DAF=180°,此时D、A、F三点在同一条直线上,以A,D,E,F为顶点的四边形就不存在.
(1)证明:∵△ABD,△BCE都是等边三角形,
∴∠DBE=∠ABC=60°-∠ABE,AB=BD,BC=BE.
在△ABC和△DBE中
 ,
,
∴△ABC≌△DBE(SAS).
∴DE=AC.
又∵AC=AF,
∴DE=AF.
同理可得EF=AD.
∴四边形ADEF是平行四边形.
(2)∵四边形ADEF是平行四边形,
∴当∠DAF=90°时,四边形ADEF是矩形,
∴∠FAD=90°.
∴∠BAC=360°-∠DAF-∠DAB-∠FAC=360°-90°-60°-60°=150°.
则当∠BAC=150°时,四边形ADEF是矩形;
故答案为:∠BAC=150°;
(3)当AB=AC且∠BAC≠60°时,四边形ADEF是菱形,
理由是:由(1)知:AD=AB=EF,AC=DE=AF,
∵AC=AB,
∴AD=AF,
∵四边形ADEF是平行四边形,AD=AF,
∴平行四边形ADEF是菱形.
故答案为:AB=AC且∠BAC≠60°(或AB=AC≠BC);
(4)当∠BAC=60°时,∠DAF=180°,
此时D、A、F三点在同一条直线上,以A,D,E,F为顶点的四边形就不存在;
故答案为:∠BAC=60°.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:
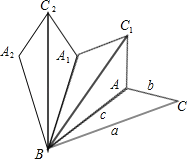
【题目】在△ABC中,∠ABC<20°,三边长分别为a,b,c,将△ABC沿直线BA翻折,得到△ABC1;然后将△ABC1沿直线BC1翻折,得到△A1BC1;再将△A1BC1沿直线A1B翻折,得到△A1BC2;…,若翻折4次后,得到图形A2BCAC1A1C2的周长为a+c+5b,则翻折11次后,所得图形的周长为_____________.(结果用含有a,b,c的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
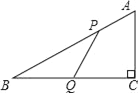
【题目】如图,在△ABC中,∠C=90°,AB=10,BC=8,P、Q分别是AB、BC边上的点,且AP=BQ=a (其中0<a<8).
(1)若PQ⊥BC,求a的值;
(2)若PQ=BQ,把线段CQ绕着点Q旋转180°,试判别点C的对应点C’是否落在线段QB上?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
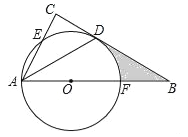
【题目】如图,点O为Rt△ABC斜边AB上一点,以OA为半径的⊙O与BC相切于点D,与AC相交于点E,与AB相交于点F,连接AD.
(1)求证:AD平分∠BAC;
(2)若点E为弧AD的中点,探究线段BD,CD之间的数量关系,并证明你的结论;
(3)若点E为弧AD的中点,CD=![]() ,求弧DF与线段BD,BF所围成的阴影部分的面积.
,求弧DF与线段BD,BF所围成的阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果批发商欲将A市的一批水果运往B市销售,有火车和汽车两种运输工具,运输过程中的损耗均为160元/时。有关数据如下:
运输工具 | 平均速度(千米/时) | 运费(元/千米) | 装卸费(元) |
火车 | 100 | 18 | 1800 |
汽车 | 80 | 22 | 1000 |
(1)如果汽车的总支出费用比火车费用多960元,求出A市与B市之间的路程是多少千米?请列方程解答。
(2)如果A市与C市之间的距离为300千米,要想将这批水果运往C市销售。选择哪种运输工具比较合算呢?请通过计算说明你的理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(探索新知)
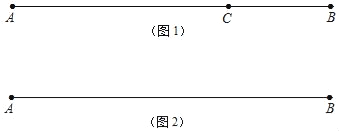
如图1,点C在线段AB上,图中共有3条线段:AB、AC和BC,若其中有一条线段的长度是另一条线段长度的两倍,则称点C是线段AB的“二倍点”.
(1)一条线段的中点 这条线段的“二倍点”;(填“是”或“不是”)
(深入研究)
如图2,若线段AB=20cm,点M从点B的位置开始,以每秒2cm的速度向点A运动,当点M到达点A时停止运动,运动的时间为t秒.
(2)问t为何值时,点M是线段AB的“二倍点”;
(3)同时点N从点A的位置开始,以每秒1cm的速度向点B运动,并与点M同时停止.请直接写出点M是线段AN的“二倍点”时t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为矩形,△ACE为AC为底的等腰直角三角形,连接BE交AD、AC分别于F. N,CM平分∠ACB交BN于M,下列结论:(1)BE⊥ED;(2)AB=AF;(3)EM=EA;(4)AM平分∠BAC,其中正确的结论有( )
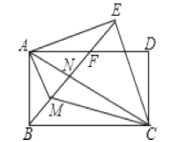
A. 1个B. 2个
C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
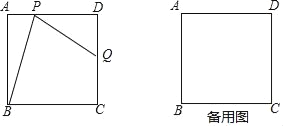
【题目】如图,在边长为2的正方形ABCD中,点P是边AD上的动点(点P不与点A、点D重合),点Q是边CD上一点,联结PB、PQ,且∠PBC=∠BPQ.
(1)当QD=QC时,求∠ABP的正切值;
(2)设AP=x,CQ=y,求y关于x的函数解析式;
(3)联结BQ,在△PBQ中是否存在度数不变的角?若存在,指出这个角,并求出它的度数;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
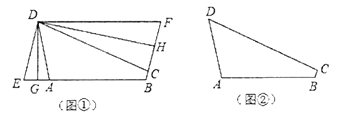
【题目】定义:有三个角相等的四边形叫做三等角四边形.
(1)在三等角四边形![]() 中,
中,![]() ,则
,则![]() 的取值范围为________.
的取值范围为________.
(2)如图①,折叠平行四边形![]() ,使得顶点
,使得顶点![]() 、
、![]() 分别落在边
分别落在边![]() 、
、![]() 上的点
上的点![]() 、
、![]() 处,折痕为
处,折痕为![]() 、
、![]() .求证:四边形
.求证:四边形![]() 为三等角四边形;
为三等角四边形;
(3)如图②,三等角四边形![]() 中,
中,![]() ,若
,若![]() ,
,![]() ,
,![]() ,则
,则![]() 的长度为多少?
的长度为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com