
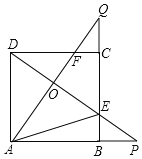
【题目】如图,正方形ABCD的边长是![]() ,连接
,连接![]() 交于点O,并分别与边
交于点O,并分别与边![]() 交于点
交于点![]() ,连接AE,下列结论:
,连接AE,下列结论:![]() ;
;![]() ;
;![]() ;
;![]() 当
当![]() 时,
时,![]() ,其中正确结论的个数是
,其中正确结论的个数是![]()
A. 1 B. 2 C. 3 D. 4
【答案】B
【解析】解:∵四边形ABCD是正方形,∴AD=BC,∠DAB=∠ABC=90°.∵BP=CQ,∴AP=BQ.在△DAP与△ABQ中, ,∴△DAP≌△ABQ,∴∠P=∠Q.∵∠Q+∠QAB=90°,∴∠P+∠QAB=90°,∴∠AOP=90°,∴AQ⊥DP,故①正确;
,∴△DAP≌△ABQ,∴∠P=∠Q.∵∠Q+∠QAB=90°,∴∠P+∠QAB=90°,∴∠AOP=90°,∴AQ⊥DP,故①正确;
∵∠DOA=∠AOP=90°,∠ADO+∠P=∠ADO+∠DAO=90°,∴∠DAO=∠P,∴△DAO∽△APO,∴![]() =
=![]() ,即AO2=ODOP.∵AE>AB,∴AE>AD,∴OD≠OE,∴OA2≠OEOP,故②错误;
,即AO2=ODOP.∵AE>AB,∴AE>AD,∴OD≠OE,∴OA2≠OEOP,故②错误;
在△CQF与△BPE中, ,∴△CQF≌△BPE,∴CF=BE,∴DF=CE.在△ADF与△DCE中,
,∴△CQF≌△BPE,∴CF=BE,∴DF=CE.在△ADF与△DCE中, ,∴△ADF≌△DCE,∴S△ADF﹣S△DFO=S△DCE﹣S△DOF,即S△AOD=S四边形OECF,故③正确;
,∴△ADF≌△DCE,∴S△ADF﹣S△DFO=S△DCE﹣S△DOF,即S△AOD=S四边形OECF,故③正确;
∵BP=1,AB=3,∴AP=4.∵△PBE∽△PAD,∴![]() =
=![]() =
=![]() ,∴BE=
,∴BE=![]() ,∴QE=
,∴QE=![]() .∵∠QOE=∠POA,∠P=∠Q,∴△QOE∽△POA,∴
.∵∠QOE=∠POA,∠P=∠Q,∴△QOE∽△POA,∴![]() =
=![]() =
=![]() =
=![]() ,即tan∠OAE=
,即tan∠OAE=![]() ,故④错误.
,故④错误.
故选B.



 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:初中数学 来源: 题型:
【题目】观察下表:

我们把表格中字母的和所得的多项式称为"'特征多项式",例如:第1格的“特征多项式”为 4x+y,第 2 格的“特征多项式”为 8x+4y, 回答下列问题:
(1)第 3 格的“特征多项式”为 第 4 格的“待征多项式”为 , 第 n 格的“特征多项式”为 .
(2)若第 m 格的“特征多项式”与多项式-24x+2y-5 的和不含有 x 项,求此“特征多项式”.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学开展以“我最喜爱的传统文化”为主题的调查活动,从“诗词、国画、对联、书法、戏曲”五种传统文化中,选取喜欢的一种(只选一种)进行调查,将调查结果整理后绘制成如图所示的不完整统计图.

(1)本次调查共抽取了多少名学生?
(2)喜欢“书法”的有多少名学生?并补全条形统计图;
(3)求喜欢“国画”对应扇形圆心角的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
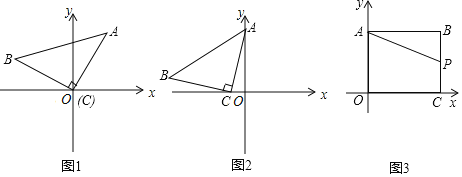
【题目】![]() 操作思考:如图1,在平面直角坐标系中,等腰
操作思考:如图1,在平面直角坐标系中,等腰![]() 的直角顶点C在原点,将其绕着点O旋转,若顶点A恰好落在点
的直角顶点C在原点,将其绕着点O旋转,若顶点A恰好落在点![]() 处
处![]() 则
则![]() 的长为______;
的长为______;![]() 点B的坐标为______
点B的坐标为______![]() 直接写结果
直接写结果![]()
![]() 感悟应用:如图2,在平面直角坐标系中,将等腰
感悟应用:如图2,在平面直角坐标系中,将等腰![]() 如图放置,直角顶点
如图放置,直角顶点![]() ,点
,点![]() ,试求直线AB的函数表达式.
,试求直线AB的函数表达式.
![]() 拓展研究:如图3,在直角坐标系中,点
拓展研究:如图3,在直角坐标系中,点![]() ,过点B作
,过点B作![]() 轴,垂足为点A,作
轴,垂足为点A,作![]() 轴,垂足为点C,P是线段BC上的一个动点,点Q是直线
轴,垂足为点C,P是线段BC上的一个动点,点Q是直线![]() 上一动点
上一动点![]() 问是否存在以点P为直角顶点的等腰
问是否存在以点P为直角顶点的等腰![]() ,若存在,请求出此时P的坐标,若不存在,请说明理由.
,若存在,请求出此时P的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形 ![]() 中,点
中,点 ![]() ,点
,点 ![]() 分别在
分别在 ![]() 轴,
轴,![]() 轴上,
轴上,![]() 为边
为边 ![]() 上的一动点,现把
上的一动点,现把 ![]() 沿
沿 ![]() 对折,
对折,![]() 点落在点
点落在点 ![]() 处.已知点
处.已知点 ![]() 的坐标为
的坐标为 ![]() .
.

(1) 当 ![]() 点坐标为
点坐标为 ![]() 时,求
时,求 ![]() 点的坐标;
点的坐标;
(2) 在点 ![]() 沿
沿 ![]() 从点
从点 ![]() 运动至点
运动至点 ![]() 的过程中,设点
的过程中,设点 ![]() 经过的路径长度为
经过的路径长度为 ![]() ,求
,求 ![]() 的值;
的值;
(3) 在点 ![]() 沿
沿 ![]() 从点
从点 ![]() 运动至点
运动至点 ![]() 的过程中,若点
的过程中,若点 ![]() 落在同一条直线
落在同一条直线 ![]() 上的次数为
上的次数为 ![]() 次,请直接写出
次,请直接写出 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)把(a﹣b)2看成一个整体,合并3(a﹣b)2﹣7(a﹣b)2+2(a﹣b)2的结果是 ;
(2)已知a+b=5(a﹣b),代数式![]() = ;
= ;
(3)已知:xy+x=﹣6,y﹣xy=2,求2[x+(xy﹣y)2]﹣3[(xy﹣y)2﹣y]﹣xy的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电器商场销售A、B两种型号计算器,两种计算器的进货价格分别为每台30元,40元,商场销售5台A型号和1台B型号计算器,可获利润76元;销售6台A型号和3台B型号计算器,可获利润120元.求商场销售A、B两种型号计算器的销售价格分别是多少元?(利润=销售价格﹣进货价格)
查看答案和解析>>
科目:初中数学 来源: 题型:
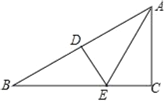
【题目】如图,在△ABC中,∠B=30°,边AB的垂直平分线分别交AB和BC于点D,E,且AE平分∠BAC.
(1)求∠C的度数;
(2)若CE=1,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
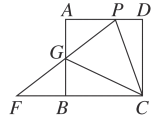
【题目】(1)如图,正方形ABCD中,∠PCG=45°,且PD=BG,求证:FP=FC.
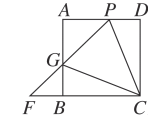
(2)如图,正方形ABCD中,∠PCG=45°,延长PG交CB的延长线于点F,(1)中的结论还成立吗?请说明理由.
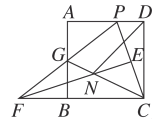
(3)在(2)的条件下,作FE⊥PC,垂足为E,交CG于点N,连接DN,求∠NDC的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com