练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图：在Rt△ABC中，AB=AC，∠BAC=90°，O为BC的中点．

    （1）写出点O到△ABC的三个顶点A、B、C距离之间的关系；

    （2）如果点M、N分别在线段AB、AC上移动，移动中保持AN=BM，请判断△OMN的形状，并证明你的结论．


           解：（1）∵在Rt△ABC中，∠BAC=90°，O为BC的中点，

    ∴OA=BC=OB=OC，

    即OA=OB=OC；

    （2）△OMN是等腰直角三角形．理由如下：

    连接AO

    ∵AC=AB，OC=OB

    ∴OA=OB，∠NAO=∠B=45°，

    在△AON与△BOM中

    ∴△AON≌△BOM（SAS）

    ∴ON=OM，∠NOA=∠MOB

    ∴∠NOA+∠AOM=∠MOB+∠AOM

    ∴∠NOM=∠AOB=90°，

    ∴△OMN是等腰直角三角形．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    抛物线y=﹣x2+bx+c的部分图象如图所示，要使y＞0，则x的取值范围是(     )

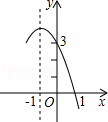
        A．﹣4＜x＜1        B．﹣3＜x＜1        C．x＜﹣4或x＞1 D．x＜﹣3或x＞1

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图：点C是∠AOB的边OB上的一点，按下列要求画图并回答问题．

    （1）过C点画OB的垂线，交OA于点D；

    （2）过C点画OA的垂线，垂足为E；

    （3）比较线段CE，OD，CD的大小（请直接写出结论）；

    （4）请写出第（3）小题图中与∠AOB互余的角（不增添其它字母）．

    　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在△ABC中，AB=AC，AD⊥BC，垂足为D，E是AC的中点．若DE=5，则AB的长为__________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在第1个△ABA1中，∠B=20°，AB=A1B，在A1B上取一点C，延长AA1到A2，使得A1A2=A1C；在A2C上取一点D，延长A1A2到A3，使得A2A3=A2D；…，按此作法进行下去，第n个三角形的以An为顶点的内角的度数为__________．

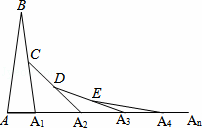
    查看答案和解析>>

    科目：初中数学 来源： 题型：


    小明和小丽是同班同学，小明的家距学校2千米远，小丽的家距学校5千米远，设小明家距小丽家x千米远，则x的值应满足（　　）

    　 A． x=3 B． x=7 C． x=3或x=7 D． 3≤x≤7

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    某商品的标价比成本价高m%，根据市场需要，该商品需降价n%出售，为了不亏本，n应满足（　　）

    　 A． n≤m B． n≤ C． n≤ D． n≤

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    下列实数大小关系判定正确的是（　　）

    　 A． ﹣0.1＞﹣0.01 B． 0＞|﹣100| C． |﹣10|＜﹣|+10| D．

    　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    若棱长为10cm的立方体的体积减少Vcm3而保存立方体形状不变，则棱长应该减少　　　　　　cm．

    查看答案和解析>>

    同步练习册答案