
【题目】如图1,在![]() 中,
中,![]() ,
,![]() .如图2,将
.如图2,将![]() 向上翻折,使点
向上翻折,使点![]() 落在
落在![]() 上,记为点
上,记为点![]() ,折痕为
,折痕为![]() .过
.过![]() 点作
点作![]() 平行线交
平行线交![]() 延长线于点
延长线于点![]() ,连接
,连接![]() .
.
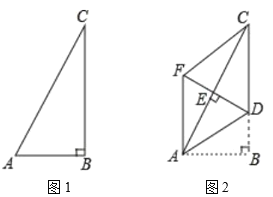
(1)证明:四边形![]() 是菱形.
是菱形.
(2)若![]() ,求
,求![]() 的长度.
的长度.
【答案】(1)见解析;(2)2![]()
【解析】
(1)利用含30度角的直角三角形的性质得到AC=2AB,利用翻折的性质得到AE=AB,DE⊥AC,再证明△AEF![]() △CED,EF=DE,根据对角线互相垂直平分的四边形是菱形即可证得结论;
△CED,EF=DE,根据对角线互相垂直平分的四边形是菱形即可证得结论;
(2)利用(1)的结论结合三角函数的知识,即可求得DE的长,从而求得DF的长度.
(1)在![]() 中,
中,![]() ,
,![]() .
.
∴AC=2AB,
由折叠的性质得:∠AED=∠B=90°,AE=AB,
∴AC⊥DF,
∵AC=2AB,
∴CE=AB=AE,
∵AF∥CD,
∴∠FAE=∠DCE,
在△AEF和△CED中,
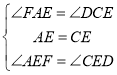 ,
,
∴△AEF![]() △CED,
△CED,
∴EF= ED,
又∵CE =AE,AC⊥DF,
∴四边形![]() 是菱形;
是菱形;
(2)由(1)得:AC=2AB=2 AE,
∴AE=3,
由折叠的性质得:∠EAD=∠BAD=![]() (90°-∠ACB)= 30°,
(90°-∠ACB)= 30°,
∵![]() ,即
,即![]() ,
,
∴DE=![]() ,
,
∴DF= 2DE=2![]() .
.


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:
【题目】嘉淇乘坐一艘游船出海游玩,游船上的雷达扫描探测得到的结果如图所示,每相邻两个圆之间距离是1km (最小圆的半径是1km ),下列关于小艇 A , B 的位置描述,正确的是( )

A.小艇 A 在游船的北偏东60°方向上,且与游船的距离是3km
B.游船在小艇 A 的南偏西60°方向上,且与小艇 A 的距离是3km
C.小艇 B 在游船的北偏西30°方向上,且与游船的距离是 2km
D.游船在小艇 B 的南偏东60°方向上,且与小艇 B 的距离是 2km
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形![]() 的边长为
的边长为![]() ,
,![]() 在正方形外,
在正方形外,![]() ,过
,过![]() 作
作![]() 于
于![]() ,直线
,直线![]() ,
,![]() 交于点
交于点![]() ,直线
,直线![]() 交直线
交直线![]() 于点
于点![]() ,则下列结论正确的是( )
,则下列结论正确的是( )

①![]() ;②
;②![]() ;③
;③![]() ;
;
④若![]() ,则
,则![]()
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ACB中,∠ACB=90°,AC=BC,点D是AB上的一个动点(不与点A,B重合),连接CD,将CD绕点C顺时针旋转90°得到CE,连接DE,DE与AC相交于点F,连接AE,则图中与△ACE全等或相似的三角形有( )
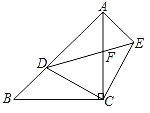
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,正方形![]() 与正方形
与正方形![]() 有公共的顶点
有公共的顶点![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,
,![]() .
.
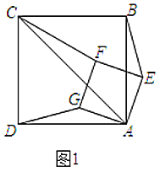
①求证:![]() ;
;
②求![]() 的值;
的值;
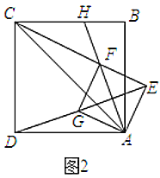
(2)将图1中的正方形![]() 旋转到图2的位置,当
旋转到图2的位置,当![]() ,
,![]() ,
,![]() 在一条直线上,若
在一条直线上,若![]() ,求正方形
,求正方形![]() 的边长.
的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC为直角三角形,∠C=90°,BC=2cm,∠A=30°,四边形DEFG为矩形,DE=2![]() cm,EF=6cm,且点C、B、E、F在同一条直线上,点B与点E重合.Rt△ABC以每秒1cm的速度沿矩形DEFG的边EF向右平移,当点C与点F重合时停止.设Rt△ABC与矩形DEFG的重叠部分的面积为ycm2,运动时间xs.能反映ycm2与xs之间函数关系的大致图象是( )
cm,EF=6cm,且点C、B、E、F在同一条直线上,点B与点E重合.Rt△ABC以每秒1cm的速度沿矩形DEFG的边EF向右平移,当点C与点F重合时停止.设Rt△ABC与矩形DEFG的重叠部分的面积为ycm2,运动时间xs.能反映ycm2与xs之间函数关系的大致图象是( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋中装有三个小球,上面分别标有数字3、4、5,这些小球除数字不同外其余均相同.
(1)从口袋中随机摸出一个小球,小球上的数字是偶数的概率是______.
(2)从口袋中随机摸出一个小球,记下数字后放回,再随机摸出一个小球,记下数字,请用画树状图(或列表)的方法,求两次摸出的小球上的数字都是奇数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
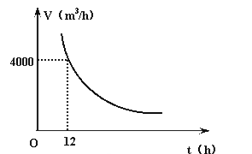
【题目】如图所示是某一蓄水池每小时的排水量V(m3/h)与排完水池中的水所用的时间t(h)之间的函数关系图象.
(1)请你根据图象提供的信息求出此蓄水池的总蓄水量;
(2)写出此函数的解析式;
(3)若要6 h排完水池中的水,那么每小时的排水量应该是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实践:如图△ABC是直角三角形,∠ACB=90°,利用直尺和圆规按下列要求作图,并在图中标明相应的字母.(保留作图痕迹,不写作法)
(1)作∠BAC的平分线,交BC于点O.
(2)以O为圆心,OC为半径作圆.
综合运用:在你所作的图中,
(1)AB与⊙O的位置关系是_____ .(直接写出答案)
(2)若AC=5,BC=12,求⊙O 的半径.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com