
【题目】如图,AB是⊙O的一条弦,点C是⊙O上一动点,且∠ACB=30°,点E、F分别是AC、BC的中点,直线EF与⊙O交于G、H两点,若⊙O的半径为10,则GE+FH的最大值为( )
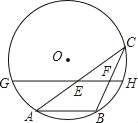
A. 5 B. 10 C. 15 D. 20
【答案】C
【解析】
首先连接OA、OB,根据圆周角定理,求出∠AOB=2∠ACB=60°,进而判断出△AOB为等边三角形;然后根据⊙O的半径为5,可得AB=OA=OB=5,再根据三角形的中位线定理,求出EF的长度;最后判断出当弦GH是圆的直径时,它的值最大,进而求出GE+FH的最大值是多少即可.
如图1,连接OA、OB,
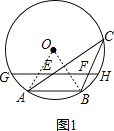 ,
,
∵∠ACB=30°,
∴∠AOB=2∠ACB=60°,
∵OA=OB,
∴△AOB为等边三角形,
∵⊙O的半径为10,
∴AB=OA=OB=10,
∵点E,F分别是AC、BC的中点,
∴EF=![]() AB=5,
AB=5,
要求GE+FH的最大值,即求GE+FH+EF(弦GH)的最大值,
∵当弦GH是圆的直径时,它的最大值为:10×2=20,
∴GE+FH的最大值为:20-5=15.
故选C.


科目:初中数学 来源: 题型:
【题目】如图,在足够大的空地上有一段长为![]() 米的旧墙
米的旧墙![]() ,某人利用旧墙和木栏围成一个矩形菜园
,某人利用旧墙和木栏围成一个矩形菜园![]()
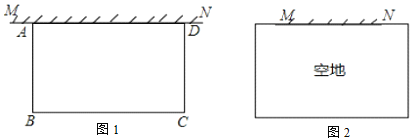
(1)如图1其中![]() ,已知矩形菜园的一边靠墙,另三边一共用了
,已知矩形菜园的一边靠墙,另三边一共用了![]() 米木栏.
米木栏.
①若![]() ,所围成的矩形菜园的面积为
,所围成的矩形菜园的面积为![]() 平方米,求所利用旧墙
平方米,求所利用旧墙![]() 的长;
的长;
②求矩形菜园![]() 面积的最大值.
面积的最大值.
(2)如图2,若![]() ,则旧墙与木栏能围成的矩形菜园
,则旧墙与木栏能围成的矩形菜园![]() 面积的最大值是多少?
面积的最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)阅读理解:实数![]() ,
, ![]() ,∵
,∵![]() ,∴
,∴![]() ,即
,即![]() 。若
。若![]() (
(![]() 为定值),则
为定值),则![]() ,当且仅当
,当且仅当![]() 时等式成立,即
时等式成立,即![]() 时,
时, ![]() ,∴当
,∴当![]() 时,
时, ![]() 取得 值(填“最大”或“最小”)。
取得 值(填“最大”或“最小”)。
(2)理解应用:函数![]() ,当x= 时,
,当x= 时, ![]() 。
。
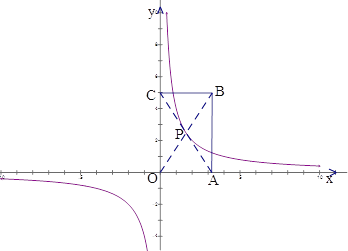
(3)拓展应用:如图,双曲线![]() 经过矩形OABC的对角线交点P,求矩形OABC的最小周长。
经过矩形OABC的对角线交点P,求矩形OABC的最小周长。
查看答案和解析>>
科目:初中数学 来源: 题型:
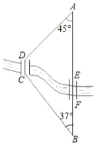
【题目】如图,A,B两地之间有条河,原来从A地到B地需要经过桥DC,沿折线A→D→C→B到达,现在新建了桥EF,可直接沿直线AB从A地到达B地.已知BC=11km,∠A=45°,∠B=37°,桥DC和AB平行,桥DC与桥EF的长相等.
(1)求点D到直线AB的距离;
(2)现在从A地到B地可比原来少走多少路程?
(结果保留小数点后一位.参考数据:![]() ≈1.41,sin37°≈0.60,cos37°≈0.80).
≈1.41,sin37°≈0.60,cos37°≈0.80).
查看答案和解析>>
科目:初中数学 来源: 题型:
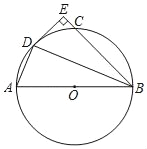
【题目】如图,AB为⊙O的直径,C为⊙O上一点,∠ABC的平分线交⊙O于点D,DE⊥BC于点E.
(1)试判断DE与⊙O的位置关系,并说明理由;
(2)若⊙O的半径为3,BC=4,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有四张正面分别标有数字﹣1,0,1,2的不透明卡片,它们除数字外其余全部相同,现将它们背面朝上洗均匀.
(1)随机抽取一张卡片,求抽到数字“﹣1”的概率;
(2)随机抽取一张卡片,然后不放回,再随机抽取一张卡片,请用列表或画树状图的方法求出第一次抽到数字“2”且第二次抽到数字“0”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】城市中“打车难”一直是人们关注的一个社会热点问题.近几年来,“互联网+”战略与传统出租车行业深度融合,“优步”、“滴滴出行”等打车软件就是其中典型的应用,名为“数据包络分析”(简称DEA)的一种效率评价方法,可以很好地优化出租车资源配置,为了解出租车资源的“供需匹配”,北京、上海等城市对每天24个时段的DEA值进行调查,调查发现,DEA值越大,说明匹配度越好.在某一段时间内,北京的DEA值y与时刻t的关系近似满足函数关系![]() (a,b,c是常数,且
(a,b,c是常数,且![]() ≠0),如图记录了3个时刻的数据,根据函数模型和所给数据,当“供需匹配”程度最好时,最接近的时刻t是( )
≠0),如图记录了3个时刻的数据,根据函数模型和所给数据,当“供需匹配”程度最好时,最接近的时刻t是( )
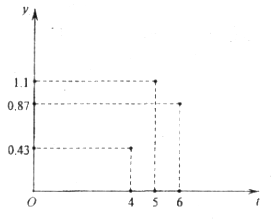
A. 4.8 B. 5 C. 5.2 D. 5.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c经过点(﹣1,0),对称轴l如图所示,则下列结论:①abc>0;②a﹣b+c=0;③2a+c<0;④a+b<0,其中所有正确的结论是( )

A.①③ B.②③ C.②④ D.②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com