
【题目】如图,在足够大的空地上有一段长为![]() 米的旧墙
米的旧墙![]() ,某人利用旧墙和木栏围成一个矩形菜园
,某人利用旧墙和木栏围成一个矩形菜园![]()
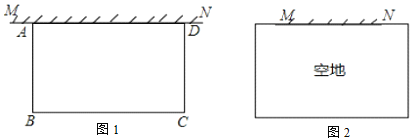
(1)如图1其中![]() ,已知矩形菜园的一边靠墙,另三边一共用了
,已知矩形菜园的一边靠墙,另三边一共用了![]() 米木栏.
米木栏.
①若![]() ,所围成的矩形菜园的面积为
,所围成的矩形菜园的面积为![]() 平方米,求所利用旧墙
平方米,求所利用旧墙![]() 的长;
的长;
②求矩形菜园![]() 面积的最大值.
面积的最大值.
(2)如图2,若![]() ,则旧墙与木栏能围成的矩形菜园
,则旧墙与木栏能围成的矩形菜园![]() 面积的最大值是多少?
面积的最大值是多少?
【答案】(1)①![]() ;②I 当
;②I 当![]() 时,
时,![]() 的最大值为
的最大值为![]() ;II 当
;II 当![]() 时,
时,![]() 的范围为
的范围为![]() ,
,![]() 的最大值为
的最大值为![]() ;(2)
;(2)![]() 时,
时,![]() 的最大值为
的最大值为![]() .
.
【解析】
(1)①设AB=xm,则BC=(100-2x)m,利用矩形的面积公式得到x(100-2x)=450,解方程得x1=5,x2=45,然后计算100-2x后与20进行大小比较即可得到AD的长;
②设AD=xm,利用矩形面积得到S=![]() x(100-x),配方得到S=-
x(100-x),配方得到S=-![]() (x-50)2+1250,讨论:当a≥50时,根据二次函数的性质得S的最大值为1250m2;当0<a<50时,则当0<x≤a时,根据二次函数的性质得S的最大值为50a-
(x-50)2+1250,讨论:当a≥50时,根据二次函数的性质得S的最大值为1250m2;当0<a<50时,则当0<x≤a时,根据二次函数的性质得S的最大值为50a-![]() a2.
a2.
(2)根据题意列出函数关系式,根据二次函数的性质即可得到结论.
(1)设AB=xm,则BC=(100-2x)m,
根据题意得x(100-2x)=450,解得x1=5,x2=45,
当x=5时,100-2x=90>20,不合题意舍去;
当x=45时,100-2x=10,
答:AD的长为10m;
(2)设AD=xm,
∴S=![]() x(100-x)=-
x(100-x)=-![]() (x-50)2+1250,
(x-50)2+1250,
当a≥50时,则x=50时,S的最大值为1250;
当0<a<50时,则当0<x≤a时,S随x的增大而增大,当x=a时,S的最大值为50a-![]() a2,
a2,
综上所述,当a≥50时,S的最大值为1250m2;当0<a<50时,S的最大值为(50a-![]() a2)m2.
a2)m2.
(2)设四边形ABCD的面积为W,AD=x,则AB=60-x,
∴W=x(60-x)=-(x-30)2+900(10<x<60),
∴当x=30时,矩形菜园ABCD面积的最大值是900m2.
故答案为:900.


科目:初中数学 来源: 题型:
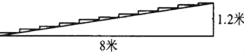
【题目】每年的5月15日是”世界助残日”,某商场门前的台阶共高出地面1.2米,为帮助残疾人,便于轮椅行走,准备拆除台阶换成斜坡,又考虑安全,轮椅行走斜坡的坡角不得超过9°,已知此商场门前的人行道距门前垂直距离为8米(斜坡不能修在人行道上),问此商场能否把台阶换成斜坡?(参考数据sin9°=0.1564,cos9°=0.9877,tan9°=0.1584)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,用长为6m的铝合金条制成“日”字形窗框,若窗框的宽为xm,窗户的透光面积为ym2(铝合金条的宽度不计).
(1)求出y与x的函数关系式;
(2)如何安排窗框的长和宽,才能使得窗户的透光面积最大?并求出此时的最大面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若一个三角形一条边的平方等于另两条边的乘积,我们把这个三角形叫做比例三角形.

![]() 已知
已知![]() 是比例三角形,
是比例三角形,![]() ,
,![]() ,请直接写出所有满足条件的AC的长;
,请直接写出所有满足条件的AC的长;
![]() 如图1,在四边形ABCD中,
如图1,在四边形ABCD中,![]() ,对角线BD平分
,对角线BD平分![]() ,
,![]() 求证:
求证:![]() 是比例三角形.
是比例三角形.
![]() 如图2,在
如图2,在![]() 的条件下,当
的条件下,当![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
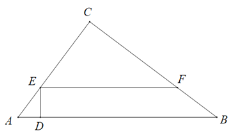
【题目】如图,在直角△ABC中,∠C=90°,AC=15,BC=20,点D为AB边上一动点,若AD的长度为m,且m的范围为0<m<9,在AC与BC边上分别取两点E、F,满足ED⊥AB,FE⊥ED.
(1)求DE的长度;(用含m的代数式表示)
(2)求EF的长度;(用含m的代数式表示)
(3)请根据m的不同取值,探索过D、E、F三点的圆与△ABC三边交点的个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y1=x2+mx+n的图象经过点P(﹣3,1),对称轴是经过(﹣1,0)且平行于y轴的直线.
(1)求m,n的值.
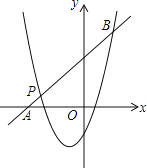
(2)如图,一次函数y2=kx+b的图象经过点P,与x轴相交于点A,与二次函数的图象相交于另一点B,点B在点P的右侧,PA:PB=1:5,求一次函数的表达式.
(3)直接写出y1>y2时x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图像如图所示,则下列五个结论中:①albic<0;②a﹣b+c>0;③2a﹣b<0;④abc<0;⑤4a+2b+c>0,错误的个数有( )
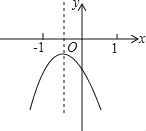
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小磊要制作一个三角形的钢架模型,在这个三角形中,长度为x(单位:cm)的边与这条边上的高之和为40 cm,这个三角形的面积S(单位:cm2)随x(单位:cm)的变化而变化.
(1)请直接写出S与x之间的函数关系式(不要求写出自变量x的取值范围);
(2)当x是多少时,这个三角形面积S最大?最大面积是多少?![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的一条弦,点C是⊙O上一动点,且∠ACB=30°,点E、F分别是AC、BC的中点,直线EF与⊙O交于G、H两点,若⊙O的半径为10,则GE+FH的最大值为( )
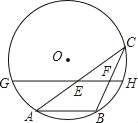
A. 5 B. 10 C. 15 D. 20
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com