
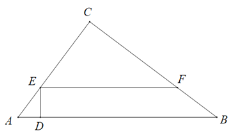
【题目】如图,在直角△ABC中,∠C=90°,AC=15,BC=20,点D为AB边上一动点,若AD的长度为m,且m的范围为0<m<9,在AC与BC边上分别取两点E、F,满足ED⊥AB,FE⊥ED.
(1)求DE的长度;(用含m的代数式表示)
(2)求EF的长度;(用含m的代数式表示)
(3)请根据m的不同取值,探索过D、E、F三点的圆与△ABC三边交点的个数.
【答案】(1)![]() ;(2) 25-
;(2) 25-![]() ; (3)见解析.
; (3)见解析.
【解析】
(1)先证△ADE∽△ACB,得到![]() =
=![]() ,代入即可得到DE=
,代入即可得到DE=![]() ;
;
(2)由勾股定理得到AE=![]() ,利用两个角相等的两个三角形相似得到△ADE∽△ECF,利用相似三角形对应边成比例,得到
,利用两个角相等的两个三角形相似得到△ADE∽△ECF,利用相似三角形对应边成比例,得到![]() =
=![]() ,代入即可得到EF=25-
,代入即可得到EF=25-![]() ;
;
(3)先分别求出过D、E、F三点的⊙O与AC和BC相切时m=![]() 和m=
和m=![]() ,再分0<m<
,再分0<m<![]() ,m=
,m=![]() ,
,![]() <m<
<m<![]() ,m=
,m=![]() ,
,![]() <m<9,五种情况进行说明.
<m<9,五种情况进行说明.
解:(1)∵ED⊥AB,∴∠EDA=90°,∴∠EDA=∠C=90°,
∵∠A=∠A,∴△ADE∽△ACB,
∴![]() =
=![]() ,∴
,∴![]() =
=![]() ,
,
∴DE=![]() ;
;
(2)在RT△ADE中,
AE=![]() =
=![]() ,
,
∵ED⊥
∴∠EDA=∠DEF=90°,
∴EF∥AB,
∴∠A=∠CEF,
又∵∠EDA=∠C,
∴△ADE∽△ECF,
∴![]() =
=![]() ,∴m:(15-
,∴m:(15-![]() )=
)=![]() :EF,
:EF,
∴EF=25-![]() .
.
(3)当ED:EF=3:4,⊙O与AC相切于点E,
![]() :(25-
:(25-![]() )=3:4,m=
)=3:4,m=![]() ,
,
当ED:EF=4:3,⊙O与BC相切于点F,
![]() :(25-
:(25-![]() )=4:3,m=
)=4:3,m=![]() ,
,
情况一:当0<m<![]() 时,⊙O与△ABC有六个交点;
时,⊙O与△ABC有六个交点;
情况二:当m=![]() 时,⊙O与△ABC有五个交点;
时,⊙O与△ABC有五个交点;
情况三:当![]() <m<
<m<![]() 时,⊙O与△ABC有六个交点;
时,⊙O与△ABC有六个交点;
情况四:当m=![]() 时,⊙O与△ABC有五个交点;
时,⊙O与△ABC有五个交点;
情况五:当![]() <m<9时,⊙O与△ABC有六个交点.
<m<9时,⊙O与△ABC有六个交点.
故答案为:(1)![]() ;(2) 25-
;(2) 25-![]() ; (3)见解析.
; (3)见解析.


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:初中数学 来源: 题型:
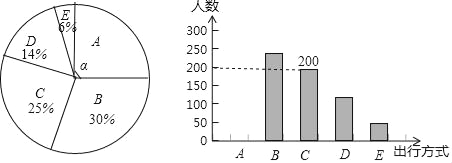
【题目】为了解某市市民“绿色出行”方式的情况,某校数学兴趣小组以问卷调查的形式,随机调查了某市部分出行市民的主要出行方式(参与问卷调查的市民都只从以下五个种类中选择一类),并将调查结果绘制成如下不完整的统计图. 根据以上信息,回答下列问题:
(1)参与本次问卷调查的市民共有 人,其中选择B类的人数有 人;
(2)在扇形统计图中,求A类对应扇形圆心角α的度数,并补全条形统计图;
(3)该市约有12万人出行,若将A,B,C这三类出行方式均视为“绿色出行”方式,请估计该市“绿色出行”方式的人数.
种类 | A | B | C | D | E |
出行方式 | 共享单车 | 步行 | 公交车 | 的士 | 私家车 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(﹣1,0),对称轴为直线x=2,下列结论:(1)4a+b=0;(2)9a+c>3b;(3)8a+7b+2c>0;(4)若点A(﹣3,y1)、点B(﹣![]() ,y2)、点C(
,y2)、点C(![]() ,y3)在该函数图象上,则y1<y3<y2;(5)若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2,且x1<x2,则x1<﹣1<5<x2.其中正确的结论有( )
,y3)在该函数图象上,则y1<y3<y2;(5)若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2,且x1<x2,则x1<﹣1<5<x2.其中正确的结论有( )

A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AD为⊙O的直径,BC为⊙O的切线,切点为M,分别过A,D两点作BC的垂线,垂足分别为B,C,AD的延长线与BC相交于点E.
(1)求证:△ABM∽△MCD;
(2)若AD=8,AB=5,求ME的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
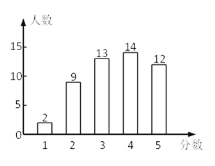
【题目】光明中学全体学生1100人参加社会实践活动,从中随机抽取50人的社会实践活动成绩制成如图所示的条形统计图,结合图中所给信息解答下列问题:
(1)填写下表:
中位数 | 众数 | |
随机抽取的50人的社会实践活动成绩(单位:分) |
(2)估计光明中学全体学生社会实践活动成绩的总分.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在足够大的空地上有一段长为![]() 米的旧墙
米的旧墙![]() ,某人利用旧墙和木栏围成一个矩形菜园
,某人利用旧墙和木栏围成一个矩形菜园![]()
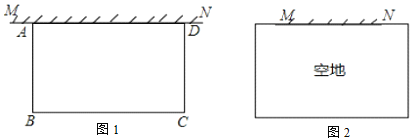
(1)如图1其中![]() ,已知矩形菜园的一边靠墙,另三边一共用了
,已知矩形菜园的一边靠墙,另三边一共用了![]() 米木栏.
米木栏.
①若![]() ,所围成的矩形菜园的面积为
,所围成的矩形菜园的面积为![]() 平方米,求所利用旧墙
平方米,求所利用旧墙![]() 的长;
的长;
②求矩形菜园![]() 面积的最大值.
面积的最大值.
(2)如图2,若![]() ,则旧墙与木栏能围成的矩形菜园
,则旧墙与木栏能围成的矩形菜园![]() 面积的最大值是多少?
面积的最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
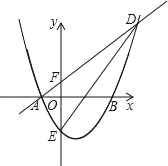
【题目】如图,抛物线![]() 与x轴交于A(-1,0)和B(3,0)两点,交y轴于点E.
与x轴交于A(-1,0)和B(3,0)两点,交y轴于点E.
(1)求此抛物线的解析式.
(2)若直线y=x+1与抛物线交于A、D两点,与y轴交于点F,连接DE,求△DEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知抛物线![]() 经过点A(0,3),B(3,0),C(4,3).
经过点A(0,3),B(3,0),C(4,3).
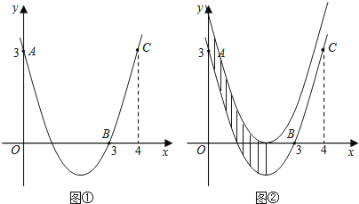
(1)求抛物线的函数表达式;
(2)求抛物线的顶点坐标和对称轴;
(3)把抛物线向上平移,使得顶点落在x轴上,直接写出两条抛物线、对称轴和y轴围成的图形的面积S(图②中阴影部分).
查看答案和解析>>
科目:初中数学 来源: 题型:
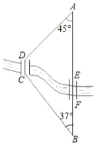
【题目】如图,A,B两地之间有条河,原来从A地到B地需要经过桥DC,沿折线A→D→C→B到达,现在新建了桥EF,可直接沿直线AB从A地到达B地.已知BC=11km,∠A=45°,∠B=37°,桥DC和AB平行,桥DC与桥EF的长相等.
(1)求点D到直线AB的距离;
(2)现在从A地到B地可比原来少走多少路程?
(结果保留小数点后一位.参考数据:![]() ≈1.41,sin37°≈0.60,cos37°≈0.80).
≈1.41,sin37°≈0.60,cos37°≈0.80).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com