
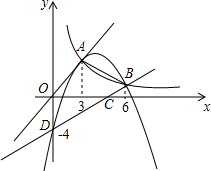
 ��ͼ����ƽ��ֱ������ϵ�У�����������y=x�ͷ���������y=$\frac{9}{x}$��ͼ���ڵ�һ�����ڵ�A
��ͼ����ƽ��ֱ������ϵ�У�����������y=x�ͷ���������y=$\frac{9}{x}$��ͼ���ڵ�һ�����ڵ�A���� ��1����������������ͷ����������Ľ���ʽ���ô���ϵ�������
��2����ΪB��Ϊ���������Ľ��㣬��B��6��m��������֪����y=$\frac{9}{x}$���������m��ֵ������һ�κ���������������ƽ�У���֪���߱���ϵ����ͬ�����ô���ϵ�������b��ֵ��
��3��A��B�����������D������ɸ���һ�κ�������ʽ��ã�����ͼ�Σ���E��������Ϊh��������κ�������ʽ���E������꼴�ɣ�
��� 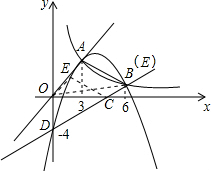 �⣺��1���������������Ľ���ʽΪy=k1x��k1��0����
�⣺��1���������������Ľ���ʽΪy=k1x��k1��0����
��Ϊy=k1x��ͼ�����A��3��3����
����3=3k1�����k1=1��
��������������Ľ���ʽΪy=x��
�跴���������Ľ���ʽΪy=$\frac{{k}^{2}}{x}$��k2��0����
��Ϊy=$\frac{{k}^{2}}{x}$ ��ͼ�����A��3��3����
����3=$\frac{{k}^{2}}{3}$��
���k2=9��
��������������Ľ���ʽΪy=$\frac{9}{x}$��
��2����Ϊ��B��6��n����y=$\frac{9}{x}$��ͼ���ϣ�
����n=$\frac{9}{6}$=$\frac{3}{2}$��
���B��6��$\frac{3}{2}$����
��һ�κ�������ʽΪy=k3x+b��k3��0����
��Ϊy=k3x+b��ͼ������y=xƽ�Ƶõ��ģ�
����k3=1����y=x+b��
����Ϊy=x+b��ͼ�����B��6��$\frac{3}{2}$ ����
����$\frac{3}{2}$=6+b��
���b=-$\frac{9}{2}$��
��һ�κ����Ľ���ʽΪy=x-$\frac{9}{2}$��
��3����ͼ����Ϊy=x-$\frac{9}{2}$��ͼ��y���ڵ�D��
����D��������0��-$\frac{9}{2}$����
����κ����Ľ���ʽΪy=ax2+bx+c��a��0����
��Ϊy=ax2+bx+c��ͼ�����A��3��3����B��6��$\frac{3}{2}$������D��0��-$\frac{9}{2}$����
����$\left\{\begin{array}{l}9a+3b+c=3\\ 36+6b+c=\frac{3}{2}\\ c=-\frac{9}{2}\end{array}\right.$��
���$\left\{\begin{array}{l}a=-\frac{1}{2}\\ b=4\\ c=-\frac{9}{2}\end{array}\right.$��
������κ����Ľ���ʽΪy=-$\frac{1}{2}$x2+4x-$\frac{9}{2}$��
��y=x-$\frac{9}{2}$��x���ڵ�C��
���C�������ǣ�$\frac{9}{2}$��0����
��E��������Ϊh��
��$\frac{1}{2}$��$\frac{9}{2}$h=$\frac{27}{8}$��
���h=$\frac{3}{2}$��
��y=$\frac{3}{2}$ʱ��-$\frac{1}{2}$x2+4x-$\frac{9}{2}$=$\frac{3}{2}$��
�����ã�x2-8x+12=0��
����x-2����x-6��=0��
x1=2��x2=6��
��E��������2��$\frac{3}{2}$������6��$\frac{3}{2}$����
���� ���⿼���˷����������ۺ��⣬��������ѧ������Ҫ������һ�κ������������������������������������κ�������������������ô���ϵ������������ʽ������������Ĺ�ϵ��������ͼ����������ۺ��Խ�ǿ���Ѷ����У�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
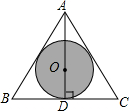 ��ͼ����֪��O�ǵȱ�������ABCֽ�������Բ��������OͿ�Ϻ�ɫ�������������ֽ����Ϊ���ӣ��������Ϸ����ÿ�η��ھ�������������ֽ���ڣ�����������һ��Ļ��ᶼ��ͬ�����ʣ��������ں�ɫ����ĸ��ʴ������ڰ�ɫ�����Ϊʲô��
��ͼ����֪��O�ǵȱ�������ABCֽ�������Բ��������OͿ�Ϻ�ɫ�������������ֽ����Ϊ���ӣ��������Ϸ����ÿ�η��ھ�������������ֽ���ڣ�����������һ��Ļ��ᶼ��ͬ�����ʣ��������ں�ɫ����ĸ��ʴ������ڰ�ɫ�����Ϊʲô���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1��$\sqrt{5}$��2 | B�� | $\sqrt{3}$��$\sqrt{4}$��$\sqrt{5}$ | C�� | 3��4��5 | D�� | 32��42��52 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com