
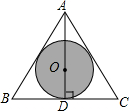
 如图,已知⊙O是等边三角形ABC纸板的内切圆,并给⊙O涂上黑色,将这块三角形纸板作为靶子,玩飞镖游戏(设每次飞镖均能落在三角形纸板内,且落在任意一点的机会都相同).问:飞镖落在黑色区域的概率大,还是落在白色区域大?为什么?
如图,已知⊙O是等边三角形ABC纸板的内切圆,并给⊙O涂上黑色,将这块三角形纸板作为靶子,玩飞镖游戏(设每次飞镖均能落在三角形纸板内,且落在任意一点的机会都相同).问:飞镖落在黑色区域的概率大,还是落在白色区域大?为什么? 分析 根据题意分别得出S⊙O以及空白面积,进而比较得出即可.
解答 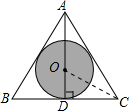 解:设BC切⊙O于点D,连接OC
解:设BC切⊙O于点D,连接OC
∵CA、CB都与⊙O相切,
∴∠OCD=∠OCA=30°;
设三角形边长为2a,
Rt△OCD中,CD=$\frac{1}{2}$BC=a,∠OCD=30°;
∴OD=CD•tan30°=$\frac{\sqrt{3}}{3}$a,则AD=$\sqrt{3}$a,
∴S⊙O=π(OD)2=$\frac{π{a}^{2}}{3}$.
则空白面积为:S△ABC-$\frac{1}{2}$×2a×$\sqrt{3}$a=$\sqrt{3}$a2-$\frac{π{a}^{2}}{3}$=($\sqrt{3}$-$\frac{π}{3}$)a2,
∵$\frac{π{a}^{2}}{3}$>($\sqrt{3}$-$\frac{π}{3}$)a2,
∴飞镖落在黑色区域的概率大.
点评 本题考查了几何概率.用到的知识点为:概率=相应的面积与总面积之比.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x≥$\frac{3}{2}$ | B. | x>$\frac{3}{2}$ | C. | x≤$\frac{3}{2}$ | D. | x<$\frac{3}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
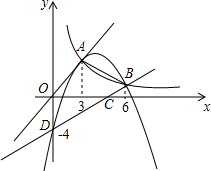 如图,在平面直角坐标系中,正比例函数y=x和反比例函数y=$\frac{9}{x}$的图象交于第一象限内点A
如图,在平面直角坐标系中,正比例函数y=x和反比例函数y=$\frac{9}{x}$的图象交于第一象限内点A查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com