
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案科目:初中数学 来源: 题型:解答题
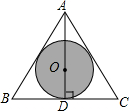 如图,已知⊙O是等边三角形ABC纸板的内切圆,并给⊙O涂上黑色,将这块三角形纸板作为靶子,玩飞镖游戏(设每次飞镖均能落在三角形纸板内,且落在任意一点的机会都相同).问:飞镖落在黑色区域的概率大,还是落在白色区域大?为什么?
如图,已知⊙O是等边三角形ABC纸板的内切圆,并给⊙O涂上黑色,将这块三角形纸板作为靶子,玩飞镖游戏(设每次飞镖均能落在三角形纸板内,且落在任意一点的机会都相同).问:飞镖落在黑色区域的概率大,还是落在白色区域大?为什么?查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com