
分析 ①把(x-1)看作一个整体,利用平方根的定义解答;
②利用“十字相乘法”对左边进行因式分解;
③把右边的项移到左边,用提公因式法因式分解求出方程的根;
④利用求根公式进行答题.
解答 解:①(x-1)2=9,
∴x-1=3或x-1=-3,
解得x1=4,x2=-2;
②由原方程,得
(x-3)(x-1)=0,
解得x1=3,x2=1;
③3(x-2)2-x(x-2)=0
(x-2)[3(x-2)-x]=0
(x-2)(2x-6)=0
x-2=0或2x-6=0
∴x1=2,x2=3;
④x2-4$\sqrt{3}$x+10=0中a=1,b=-4$\sqrt{3}$,c=10,
则△=b2-4ac=(-4$\sqrt{3}$)2-4×1×10=8,
则x=$\frac{4\sqrt{3}±2\sqrt{2}}{2}$=2$\sqrt{3}$±$\sqrt{2}$.
所以x1=2$\sqrt{3}$+$\sqrt{2}$,x2=2$\sqrt{3}$-$\sqrt{2}$.
点评 本题考查了一元二次方程的解法.解一元二次方程常用的方法有直接开平方法,配方法,公式法,因式分解法,要根据方程的特点灵活选用合适的方法.


科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $-\frac{3}{2}$ | C. | $-\frac{1}{2}$ | D. | $\frac{1}{2}$或$-\frac{3}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
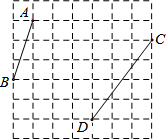 如图,在每个小正方形的边长均为1的方格纸中,有线段AB和线段CD,点A、B、C、D均在小正方形的顶点上.
如图,在每个小正方形的边长均为1的方格纸中,有线段AB和线段CD,点A、B、C、D均在小正方形的顶点上.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
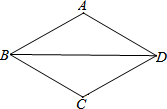 如图,△ABD≌△CBD,AB=AD,∠BAD=120°,点P从点B出发,沿线段BD向终点D运动,射线AP交折线B-C-D于点Q,当AP垂直△ABD的一腰时,PQ=2,则此时线段BP=4或8.
如图,△ABD≌△CBD,AB=AD,∠BAD=120°,点P从点B出发,沿线段BD向终点D运动,射线AP交折线B-C-D于点Q,当AP垂直△ABD的一腰时,PQ=2,则此时线段BP=4或8.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
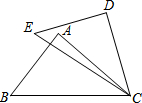 已知:如图,在△ABC与△DEC中,∠A=∠D,还需要添加两个条件才能使得△ABC≌△DEC,则错误的是( )
已知:如图,在△ABC与△DEC中,∠A=∠D,还需要添加两个条件才能使得△ABC≌△DEC,则错误的是( )| A. | AB=DE,∠B=∠E | B. | AB=DE,AC=DC | C. | BC=EC,∠BCE=∠ACD | D. | BC=EC,AC=DC |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
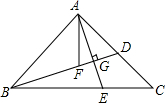 如图,在△ABC中,AB=AC,∠BAC=90°,点D是AC边上的一点,连结BD,作AE⊥BD交BC于点E,交BD于点G,AF平分∠BAC交BD于点F,试说明AE=BF的理由.
如图,在△ABC中,AB=AC,∠BAC=90°,点D是AC边上的一点,连结BD,作AE⊥BD交BC于点E,交BD于点G,AF平分∠BAC交BD于点F,试说明AE=BF的理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com