
【题目】如图(1),在矩形ABCD中,AB=4,BC=6,P是AD的中点,N是BC延长线上一点,连结PN,过点P作PN的垂线,交AB于点E,交CD的延长线于点F,连结EN,FN,设CN=x,AE=y.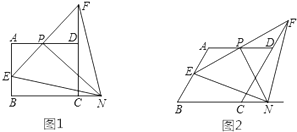
(1)求证:PE=PF;
(2)当0<x< ![]() 时,求y关于x的函数表达式;
时,求y关于x的函数表达式;
(3)若将“矩形ABCD”变为“菱形ABCD”,如图(2),AB=BC=4,∠B=60°,当0<x<3时,其它条件不变,求此时y关于x的函数表达式.
【答案】
(1)
证明:∵P是AD的中点,四边形ABCD是矩形,
∴AP=DP,∠A=∠PDF=90°,
在△APE和△DPF中,
∵ 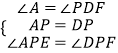 ,
,
∴△APE≌△DPF(ASA),
∴PE=PF
(2)
解:如图1,过点N作NQ⊥AD交AD延长线于Q,

∴四边形CDQN是矩形,
∴CN=DQ=x,CD=NQ=4,
又∵AD=BC=6,P是AD中点,
∴AP=PD=3,
∴PQ=3+x,
∵NP⊥EF,
∴∠APE+∠NPQ=90°,
∵∠APE+∠AEP=90°,
∴∠NPQ=∠PEA,
∵∠A=∠PQN=90°,
∴△APE∽△QNP,
∴ ![]() ,即
,即 ![]() ,
,
∴y= ![]() x+
x+ ![]()
(3)
解:如图2,过点N作NQ∥CD交AD延长线于点Q,
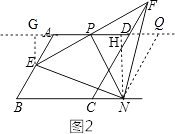
∴四边形CDQN是平行四边形,
∴CN=DQ=x,CD=NQ=4,
∵PD=PA= ![]() AD=2,
AD=2,
∴PQ=2+x,
过点N作NH⊥PQ于H,
∵∠DQN=∠DCN=∠B=60°,
∴HQ=NQcos∠DQN=4× ![]() =2,NH=NQsin∠DQN=4×
=2,NH=NQsin∠DQN=4× ![]() =2
=2 ![]() ,
,
∴PH=PQ﹣HQ=x,
过点E作EG⊥DA交DA延长线于G,
∵AE=y,∠GAE=∠B=60°,
∴AG=AEcos∠GAE= ![]() y,EG=AEsin∠GAE=
y,EG=AEsin∠GAE= ![]() y,
y,
∴PG=PA+AG=2+ ![]() y,
y,
∵∠EGP=∠PHN=∠EPN=90°,
∴∠EPG+∠PEG=∠EPG+∠NPD=90°,
∴∠PEG=∠NPD,
∴△PEG∽△NPD,
∴ ![]() ,即
,即 ![]() ,
,
∴y= ![]()
【解析】(1)证△APE≌△DPF即可得;(2)过点N作NQ⊥AD交AD延长线于Q,可得四边形CDQN是矩形,从而表示出PQ、NQ的长,再证△APE∽△QNP可得 ![]() ,据此可得函数解析式;(3)过点N作NQ∥CD交AD延长线于点Q,可得四边形CDQN是平行四边形,据此知PQ=2+x、NQ=4,再过点N作NH⊥PQ于H,由∠DQN=60°得HQ=2、NH=2
,据此可得函数解析式;(3)过点N作NQ∥CD交AD延长线于点Q,可得四边形CDQN是平行四边形,据此知PQ=2+x、NQ=4,再过点N作NH⊥PQ于H,由∠DQN=60°得HQ=2、NH=2 ![]() ,从而表示出PH的长,过点E作EG⊥DA交DA延长线于G,由AE=y、∠GAE=∠B=60°得AG、EG的长,继而可得PG的长,最后证△PEG∽△NPD得
,从而表示出PH的长,过点E作EG⊥DA交DA延长线于G,由AE=y、∠GAE=∠B=60°得AG、EG的长,继而可得PG的长,最后证△PEG∽△NPD得 ![]() ,据此即可得答案.
,据此即可得答案.


科目:初中数学 来源: 题型:
【题目】填写下列解题过程中的推理根据:
已知:如图,点F、E分别在AB、CD上,AE、DF分别与BC相交于H、G,∠A=∠D,∠1+∠2=180°.说明:AB∥CD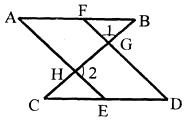
解:∵∠1=∠CGD()
∠1+∠2=180°
∴.
∴AE//FD ()
∴(两直线平行,同位角相等)
又∠A=∠D
∴∠D=∠BFD
∴()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平面直角坐标系xOy中,反比例函数![]() 的图象与一次函数y2=kx+b的图象交于点A(-4,-1)和点B(1,n).
的图象与一次函数y2=kx+b的图象交于点A(-4,-1)和点B(1,n).
(1)求这两个函数的表达式;
(2)观察图象,当y1>y2时,直接写出自变量x的取值范围;
(3)如果点C与点A关于y轴对称,求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,矩形ABCD中,AE平分∠BAD交BC于E,∠CAE=15°,则下面的结论: ①△ODC是等边三角形;②BC=2AB;③∠AOE=135°;④S△AOE=S△COE ,
其中正确结论有( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列计算中,正确的是( )
A. (﹣2a﹣5)(2a﹣5)=25﹣4a2B. (a﹣b)2=a2﹣b2
C. (x+3)(x﹣2)=x2﹣6D. ﹣a(2a2﹣1)=﹣2a3﹣a
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究与发现: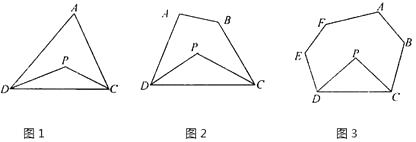
(1)探究一:三角形的一个内角与另两个内角的平分线所夹的角之间的关系
已知:如图1,在△ADC中,DP、CP分别平分∠ADC和∠ACD,
试探究∠P与∠A的数量关系,并说明理由.
(2)探究二:四边形的两个个内角与另两个内角的平分线所夹的角之间的关系
已知:如图2,在四边形ABCD中,DP、CP分别平分∠ADC和∠BCD,
试探究∠P与∠A+∠B的数量关系,并说明理由.
(3)探究三:六边形的四个内角与另两个内角的平分线所夹的角之间的关系
已知:如图3,在六边形ABCDEF中,DP、CP分别平分∠EDC和∠BCD,
请直接写出∠P与∠A+∠B+∠E+∠F的数量关系: .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com