
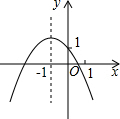
 已知二次函数y=ax2+bx+c的图象如图所示,有以下结论:
已知二次函数y=ax2+bx+c的图象如图所示,有以下结论:| A. | ①② | B. | ①③④ | C. | ①②③⑤ | D. | ①②③④⑤ |
分析 由抛物线的开口方向判断a的符号,由抛物线与y轴的交点判断c的符号,然后根据对称轴及抛物线当x=1、x=-1和x=-2时的情况进行推理,进而对所得结论进行判断.
解答 解:①当x=1时,y=a+b+c<0,故①正确;
②当x=-1时,y=a-b+c>1,故②正确;
③由抛物线的开口向下知a<0,与y轴的交点为在y轴的正半轴上,
∴c>0,对称轴为x=$\frac{b}{2a}$=-1,得2a=b,
∴a、b同号,即b<0,
∴abc>0,故③正确;
④∵对称轴为x=$\frac{b}{2a}$=-1,
∴点(0,1)的对称点为(-2,1),
∴当x=-2时,y=4a-2b+c=1,故④错误;
⑤∵x=-1时,a-b+c>1,又-$\frac{b}{2a}$=-1,即b=2a,
∴c-a>1,故⑤正确.
故选:①②③⑤.
点评 本题考查的是二次函数图象与系数的关系,掌握二次函数的性质、灵活运用数形结合思想是解题的关键,解答时,要熟练运用抛物线的对称性和抛物线上的点的坐标满足抛物线的解析式


科目:初中数学 来源: 题型:选择题
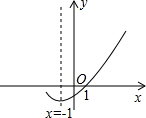 如图,是二次函数y=ax2+bx+c(a≠0)的图象的一部分,给出下列命题:
如图,是二次函数y=ax2+bx+c(a≠0)的图象的一部分,给出下列命题:| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
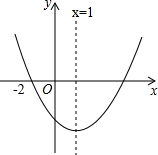 二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中:①abc<0,
二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中:①abc<0,| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
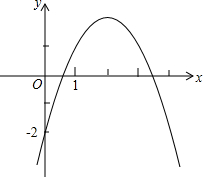 函数y=ax2+bx+c图象如图,根据图象小明做如下判断:①a<0,b>0,c>0同时成立;②函数值y≤$\frac{4ac-{b}^{2}}{4a}$;③当x$<-\frac{b}{2a}$时,y随x的增大而减小;④a+b+c>0,a-b+c<0,b2-4ac>0同时成立.判断正确的个数为( )个.
函数y=ax2+bx+c图象如图,根据图象小明做如下判断:①a<0,b>0,c>0同时成立;②函数值y≤$\frac{4ac-{b}^{2}}{4a}$;③当x$<-\frac{b}{2a}$时,y随x的增大而减小;④a+b+c>0,a-b+c<0,b2-4ac>0同时成立.判断正确的个数为( )个.| A. | 1 | B. | 2 | C. | 3 | D. | D、 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
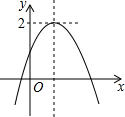 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,且关于x的一元二次方程ax2+bx+c-m=2有实数根,有下列结论:①b2-4ac>0;②abc>0;③m≤2.其中,正确结论的个数是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,且关于x的一元二次方程ax2+bx+c-m=2有实数根,有下列结论:①b2-4ac>0;②abc>0;③m≤2.其中,正确结论的个数是( )| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com