
【题目】如图,方格纸中的每个小方格都是正方形,△ABC的顶点均在格点上,建立平面直角坐标系.
(1)以原点O为对称中心,画出与△ABC关于原点O对称的△A1B1C1 , A1的坐标是
(2)将原来的△ABC绕着点(﹣2,1)顺时针旋转90°得到△A2B2C2 , 试在图上画出△A2B2C2的图形. 
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°,∠A=30°,点D,E分别在边AC,AB上,点D与点A,点C都不重合,点F在边CB的延长线上,且AE=ED=BF,连接DF交AB于点G.若BC=4,则线段EG的长为__.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在平面直角坐标系中,点P从原点O以每秒1个单位速度沿x轴正方向运动,运动时间为t秒,作点P关于直线y=tx的对称点Q,过点Q作x轴的垂线,垂足为点A.
(1)当t=2时,求AO的长.
(2)当t=3时,求AQ的长.
(3)在点P的运动过程中,用含t的代数式表示线段AP的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边三角形ABC中,AB=2,动点D从B开始沿BC向点C运动,到达点C后停止运动,将△ABD绕点A旋转后得到△ACE,则下列说法中,正确的是( )
①DE的最小值为1;②ADCE的面积是不变的;③在整个运动过程中,点E运动的路程为2;④在整个运动过程中,△ADE的周长先变小后变大.

A. ①③④ B. ①②③ C. ②③④ D. ①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校部分团员参加社会公益活动,准备购进一批许愿瓶进行销售,并将所得利润捐助给慈善机构.根据市场调查,这种许愿瓶一段时间内的销售量y (单位:个)与销售单价x(单位:元/个)之间的对应关系如图所示: 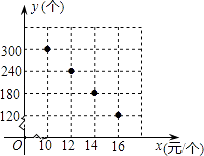
(1)y与x之间的函数关系是 .
(2)若许愿瓶的进价为6元/个,按照上述市场调查的销售规律,求销售利润w(单位:元)与销售单价x (单位:元/个)之间的函数关系式;
(3)在(2)问的条件下,若许愿瓶的进货成本不超过900元,要想获得最大利润,试确定这种许愿瓶的销售单价,并求出此时的最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=90°,AB=AC,O是BC的中点,如果在AB和AC上分别有一个动点M、N在移动,且在移动时保持AN=BM,请你判断△OMN的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD中,∠B=120°,AB=2,将图中的菱形ABCD绕点A沿逆时针方向旋转,得菱形AB′C′D′,若∠BAD′=110°,在旋转的过程中,点C经过的路线长为 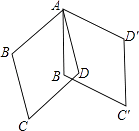
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数 ![]() 的图象经过第二象限内的点A(﹣1,m),AB⊥x轴于点B,△AOB的面积为2.若直线y=ax+b经过点A,并且经过反比例函数
的图象经过第二象限内的点A(﹣1,m),AB⊥x轴于点B,△AOB的面积为2.若直线y=ax+b经过点A,并且经过反比例函数 ![]() 的图象上另一点C(n,一2).
的图象上另一点C(n,一2).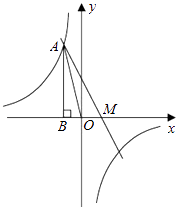
(1)求直线y=ax+b的解析式;
(2)设直线y=ax+b与x轴交于点M,求AM的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com