
| A. | 2?(-2)=-4 | B. | a?b=b?a | C. | (-2)?2=2 | D. | 若a?b=0,则a=0 |
分析 A:根据新运算a?b=a(1-b),求出2?(-2)的值是多少,即可判断出2?(-2)=-4是否正确.
B:根据新运算a?b=a(1-b),求出a?b、b?a的值各是多少,即可判断出a?b=b?a是否正确.
C:根据新运算a?b=a(1-b),求出(-2)?2的值是多少,即可判断出(-2)?2=2是否正确.
D:根据a?b=0,可得a(1-b)=0,所以a=0或b=1,据此判断即可.
解答 解:∵2?(-2)=2×[1-(-2)]=2×3=6,
∴选项A不正确;
∵a?b=a(1-b),b?a=b(1-a),
∴a?b=b?a只有在a=b时成立,
∴选项B不正确;
∵(-2)?2=(-2)×(1-2)=(-2)×(-1)=2,
∴选项C正确;
∵a?b=0,
∴a(1-b)=0,
∴a=0或b=1
∴选项D不正确.
故选:C.
点评 (1)此题主要考查了有理数的混合运算,要熟练掌握,解答此题的关键是要明确:①有理数混合运算顺序:先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算.②进行有理数的混合运算时,注意各个运算律的运用,使运算过程得到简化.
(2)此题还考查了对新运算“?”的理解和掌握,解答此题的关键是要明确:a?b=a(1-b).


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
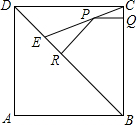 如图,E是边长为1的正方形ABCD的对角线BD上的一点,且BE=BA,P是CE上任意一点,PQ⊥BC于点Q,PR⊥BE于点R.则:(1)DE=$\sqrt{2}$-1;(2)PQ+PR=$\frac{\sqrt{2}}{2}$.
如图,E是边长为1的正方形ABCD的对角线BD上的一点,且BE=BA,P是CE上任意一点,PQ⊥BC于点Q,PR⊥BE于点R.则:(1)DE=$\sqrt{2}$-1;(2)PQ+PR=$\frac{\sqrt{2}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
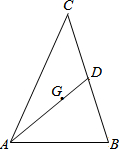 如图,G是△ABC的重心,连接AG并延长交BC于D,已知AG=2$\sqrt{3}$+2,∠BAD=45°,∠B=75°,则BC=12.
如图,G是△ABC的重心,连接AG并延长交BC于D,已知AG=2$\sqrt{3}$+2,∠BAD=45°,∠B=75°,则BC=12.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com