
【题目】综合与探究
如图,抛物线![]() 经过点
经过点![]() 、
、![]() 、
、![]() ,已知点
,已知点![]() ,
,![]() ,且
,且![]() ,点
,点![]() 为抛物线上一点(异于
为抛物线上一点(异于![]() ).
).
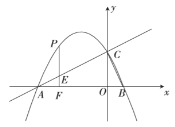
(1)求抛物线和直线![]() 的表达式.
的表达式.
(2)若点![]() 是直线
是直线![]() 上方抛物线上的点,过点
上方抛物线上的点,过点![]() 作
作![]() ,与
,与![]() 交于点
交于点![]() ,垂足为
,垂足为![]() .当
.当![]() 时,求点
时,求点![]() 的坐标.
的坐标.
(3)若点![]() 为
为![]() 轴上一动点,是否存在点
轴上一动点,是否存在点![]() ,使得由
,使得由![]() ,
,![]() ,
,![]() ,
,![]() 四点组成的四边形为平行四边形?若存在,直接写出点
四点组成的四边形为平行四边形?若存在,直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]() ,
,![]() ;(2)点
;(2)点![]() 的坐标为
的坐标为![]() ;(3)存在,点
;(3)存在,点![]() 的坐标为
的坐标为![]() 或
或![]() 或
或![]()
【解析】
(1)![]() ,则OA=4OC=8,故点A(-8,0);△AOC∽△COB,则△ABC为直角三角形,则CO2=OAOB,解得:OB=2,故点B(2,0);即可求解;
,则OA=4OC=8,故点A(-8,0);△AOC∽△COB,则△ABC为直角三角形,则CO2=OAOB,解得:OB=2,故点B(2,0);即可求解;
(2)PE=EF,即![]() ;即可求解;
;即可求解;
(3)分BC是边、BC是对角线两种情况,分别求解即可.
解:(1)∵![]() ,
,![]() ,
,
∴![]() .
.
由点![]() 的坐标可知
的坐标可知![]() ,故
,故![]() ,
,![]() ,则点
,则点![]() ,点
,点![]() .
.
设抛物线的表达式为![]() ,
,
代入点![]() 的坐标,得
的坐标,得![]() ,解得
,解得![]() .
.
故抛物线的表达式为![]()
设直线![]() 的表达式为
的表达式为![]() ,
,
代入点![]() 、
、![]() 的坐标,得
的坐标,得![]() ,解得
,解得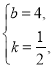
故直线![]() 的表达式为
的表达式为![]() .
.
(2)设点![]() 的坐标为
的坐标为![]() ,则点
,则点![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,
,![]() .
.
∵![]() ,
,
∴![]() ,
,
解得![]() 或
或![]() (舍去),则
(舍去),则![]() ,
,
故当![]() 时,点
时,点![]() 的坐标为
的坐标为![]() .
.
(3)设点P(m,n),n=![]() ,点M(s,0),而点B、C的坐标分别为:(2,0)、(0,4);
,点M(s,0),而点B、C的坐标分别为:(2,0)、(0,4);
①当BC是边时,
点B向左平移2个单位向上平移4个单位得到C,
同样点P(M)向左平移2个单位向上平移4个单位得到M(P),
即m-2=s,n+4=0或m+2=s,n-4=0,
解得:m=-6或±![]() -3,
-3,
故点P的坐标为:(-6,4)或(![]() -3,-4)或(-
-3,-4)或(-![]() -3,-4);
-3,-4);
②当BC是对角线时,
由中点公式得:2=m+s,n=4,
故点P(-6,4);
综上,点P的坐标为:(-6,4)或(![]() -3,-4)或(-
-3,-4)或(-![]() -3,-4).
-3,-4).


科目:初中数学 来源: 题型:
【题目】如图所示,某学校有一边长为20米的正方形![]() 区域(四周阴影是四个全等的矩形,记为区域甲;中心区是正方形
区域(四周阴影是四个全等的矩形,记为区域甲;中心区是正方形![]() ,记为区域乙).区域甲建设成休闲区,区域乙建成展示区,已知甲、乙两个区域的建设费用如下表:
,记为区域乙).区域甲建设成休闲区,区域乙建成展示区,已知甲、乙两个区域的建设费用如下表:
区域 | 甲 | 乙 |
价格(百元米2) | 6 | 5 |
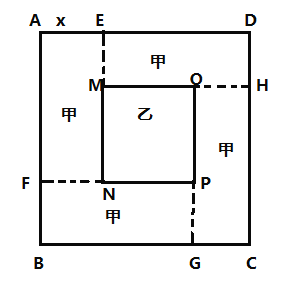
设矩形的较短边![]() 的长为
的长为![]() 米,正方形
米,正方形![]() 区域建设总费用为
区域建设总费用为![]() 百元.
百元.
(1)![]() 的长为 米(用含
的长为 米(用含![]() 的代数式表示);
的代数式表示);
(2)求![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(3)当中心区的边长要求不低于8米且不超过12米时,预备建设资金220000元够用吗?请利用函数的增减性来说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是等边三角形ABC内的一点,且PA=3,PB=4,PC=5,将△ABP绕点B顺时针旋转60°到△CBQ位置.连接PQ,则以下结论错误的是( )

A. ∠QPB=60° B. ∠PQC=90° C. ∠APB=150° D. ∠APC=135°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一元二次方程x2+2x﹣3=0的二根x1,x2(x1<x2)是抛物线y=ax2+bx+c与x轴的两个交点B,C的横坐标,且此抛物线过点A(3,6).
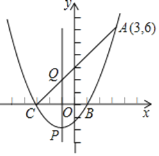
(1)求此二次函数的解析式;
(2)写出不等式ax2+bx+c≥0的解集;
(3)设此抛物线的顶点为P,对称轴与线段AC相交于点Q,求点P和点Q的坐标;
(4)在x轴上有一动点M,当MQ+MA取得最小值时,求M点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂计划生产![]() ,
,![]() 两种产品共10件,其生产成本和利润如下表.
两种产品共10件,其生产成本和利润如下表.
|
| |
成本(万元 | 2 | 5 |
利润(万元 | 1 | 3 |
(1)若工厂计划获利14万元,问![]() ,
,![]() 两种产品应分别生产多少件?
两种产品应分别生产多少件?
(2)若工厂计划投入资金不多于44万元,且获利多于22万元,问工厂有哪几种生产方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业设计了一款工艺品,每件成本40元,出于营销考虑,要求每件售价不得低于40元,但物价部门要求每件售价不得高于60元.据市场调查,销售单价是50元时,每天的销售量是100件,而销售单价每涨1元,每天就少售出2件,设单价上涨![]() 元
元![]() .
.
(1)求当![]() 为多少时每天的利润是1350元?
为多少时每天的利润是1350元?
(2)设每天的销售利润为![]() ,求销售单价为多少元时,每天利润最大?最大利润是多少?
,求销售单价为多少元时,每天利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数y=kx﹣1的图象经过点P,且y的值随x值的增大而增大,则点P的坐标可以为( )
A. (﹣5,3) B. (1,﹣3) C. (2,2) D. (5,﹣1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小刚根据以往的学习经验,想通过由“特殊到一般”的方法探究下面二次根式的运算规律.
以下是小刚的探究过程,请补充完整.
(1)具体运算,发现规律:
特例1:![]() ;特例2:
;特例2:![]() ;特例3:
;特例3:![]() ;
;
特例4:______(举一个符合上述运算特征的例子);
(2)观察、归纳,得出猜想:
如果![]() 为正整数,用含
为正整数,用含![]() 的式子表示这个运算规律:______;
的式子表示这个运算规律:______;
(3)请你证明猜想的正确性.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com