
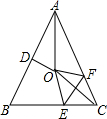
 如图,在等腰△ABC中,AB=AC,∠BAC=50°.∠BAC的平分线与线段AB的中垂线交于点O,点C沿EF折叠后与点O重合,则∠AOF的度数是( )
如图,在等腰△ABC中,AB=AC,∠BAC=50°.∠BAC的平分线与线段AB的中垂线交于点O,点C沿EF折叠后与点O重合,则∠AOF的度数是( )| A. | 105° | B. | 110° | C. | 115° | D. | 120° |
分析 连接OB,根据中垂线的性质就可以得出AO=BO,就有∠OAB=∠OBA,根据角平分线的性质就可以求出∠EBO的度数,通过△ABO≌△ACO就有BO=CO,就有∠OBC=∠OCB,再由轴对称就可以求出OF=CF,求得∠FCO=∠FOC=25°,利用三角形的外角得出∠AFO=50°,进一步利用三角形的内角和求出结论.
解答 解:如图,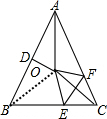
连接OB,
∵OD垂直平分AB,
∴AO=BO,
∴∠OAB=∠OBA.
∵AB=AC,∠BAC=50°
∴∠ABC=∠ACB=65°.
∵OA平分∠BAC,
∴∠BAO=∠CAO=$\frac{1}{2}$∠BAC=25°,
∴∠OBA=25°,
∴∠OBC=40°.
在△ABO和△ACO中
$\left\{\begin{array}{l}{AB=AC}\\{∠BAO=∠CAO}\\{AO=AO}\end{array}\right.$,
∴△ABO≌△ACO(SAS),
∴BO=CO,
∴∠OBC=∠OCB=40°.
∵△EOF与△ECF关于EF对称,
∴△EOF≌△ECF,
∴OF=CF,
∴∠FCO=∠FOC=25°.
∴∠AFO=50°,
∴∠AOF=180°-∠OAF-∠AFO=105°.
故选:A.
点评 本题考查了等腰三角形的性质的运用,中垂线的性质的运用,全等三角形的判定及性质的运用,轴对称的性质的运用,解答时运用全等三角形的性质及轴对称的性质求解是关键.


科目:初中数学 来源: 题型:选择题
| A. | 1组 | B. | 2组 | C. | 3组 | D. | 4组 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 月份 | 四月份 | 五月份 | 六月份 |
| 交费金额 | 30元 | 34元 | 47.8元 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m<-6 | B. | m≤-6 | C. | m>-6 | D. | m≥-6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com