【题目】如图，小明坐在堤边A处垂钓，河堤AC与水平面的夹角为30°，AC的长为
米，钓竿AO与水平线的夹角为60°，其长为3米，若AO与钓鱼线OB的夹角为60°，求浮漂B与河堤下端C之间的距离．
科目：初中数学 来源： 题型：
【题目】如图，抛物线
经过B（﹣1，0），D（﹣2，5）两点，与x轴另一交点为A，点H是线段AB上一动点，过点H的直线PQ⊥x轴，分别交直线AD、抛物线于点Q，P．
（1）求抛物线的解析式；
（2）是否存在点P，使∠APB=90°，若存在，求出点P的横坐标，若不存在，说明理由；
（3）连接BQ，一动点M从点B出发，沿线段BQ以每秒1个单位的速度运动到Q，再沿线段QD以每秒
个单位的速度运动到D后停止，当点Q的坐标是多少时，点M在整个运动过程中用时t最少？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在不透明的布袋中装有1个红球，2个白球，它们除颜色外其余完全相同．
（1）从袋中任意摸出两个球，试用树状图或表格列出所有等可能的结果，并求摸出的球恰好是两个白球的概率；
（2）若在布袋中再添加a个白球，充分搅匀，从中摸出一个球，使摸到红球的概率为
，试求a的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某灯具厂计划一天生产300盏景观灯，但由于各种原因，实际每天生产景观灯盏数与计划每天生产景观灯盏数相比有出入.下表是某周的生产情况（增产记为正，减产记为负）：
⑴求该厂这周实际生产景观灯的盏数；
⑵求该厂这周产量最多的一天比产量最少的一天多生产景观灯的盏数；
⑶该厂实出售该中灯，每盏可获得40元的利润，若把本周生产的所有灯全部销售掉，可赚多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在一个不透明的布袋里装有4个标有1，2，3，4的小球，它们的形状、大小完全相同，小明从布袋里随机取出一个小球，记下数字为x，小红在剩下的3个小球中随机取出一个小球，记下数字为y
（1）计算由x、y确定的点（x，y）在函数y=﹣x+5的图象上的概率．
（2）小明和小红约定做一个游戏，其规则为：若x、y满足xy＞6，则小明胜；若x、y满足xy＜6，则小红胜，这个游戏公平吗？请说明理由；若不公平，请写出公平的游戏规则．
查看答案和解析>>
科目：初中数学 来源： 题型：
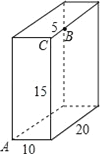
【题目】长方体的长为20cm，宽为10cm，高为15cm，点B离点C5cm，一只蚂蚁如果要沿着长方体的表面从点A爬到点B去吃一滴蜜糖，需要爬行的最短距离是多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】综合探究：如图1，在平面直角坐标系xOy中，抛物线y=﹣
+bx+8与x轴交于点A（﹣6，0）和点B（点A在点B左侧），与y轴交于点C，点P为线段AO上的一个动点，过点P作x轴的垂线l与抛物线交于点E，连接AE、EC．
（1）求抛物线的表达式及点C的坐标；
（2）连接AC交直线l于点D，则在点P运动过程中，当点D为EP中点时，S△ADP：S△CDE= ；
（3）如图2，当EC∥x轴时，点P停止运动，此时，在抛物线上是否存在点G，使得以点A、E、G为顶点的三角形是直角三角形？若存在，请求出点G的坐标，若不存在，说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读第①小题的计算方法，再计算第②小题．
①–5
+（–9
）+17
+（–3
）
解：原式=[（–5）+（–）]+[（–9）+（–）]+（17+）+[（–3+（–）]
=[（–5）+（–9）+（–3）+17]+[（–）+（–）+（–）+]
=0+（–1
）
=–1．
上述这种方法叫做拆项法．灵活运用加法的交换律、结合律可使运算简便．
②仿照上面的方法计算：（﹣2000）+（﹣1999）+4000+（﹣1）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】二次函数y=ax2+bx+c（a≠0）的图象经过点A（3，0），B（2，﹣3），并且以x=1为对称轴．
（1）求此函数的解析式；
（2）作出二次函数的大致图象；
（3）在对称轴x=1上是否存在一点P，使△PAB中PA=PB？若存在，求出P点的坐标；若不存在，说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
