
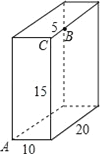
【题目】长方体的长为20cm,宽为10cm,高为15cm,点B离点C5cm,一只蚂蚁如果要沿着长方体的表面从点A爬到点B去吃一滴蜜糖,需要爬行的最短距离是多少?
【答案】需要爬行的最短距离是15![]() cm.
cm.
【解析】
首先将长方体沿CF、FG、GH剪开,向右翻折,使面FCHG和面ADCH在同一个平面内,连接AB;或将长方体沿DE、EF、FC剪开,向上翻折,使面DEFC和面ADCH在同一个平面内,连接AB,或将长方体沿CF、CH、FG剪开,向下翻折,使面HGFC和下面在同一个平面内,连接AB,然后分别在Rt△ABD与Rt△ABH与Rt△ABC,利用勾股定理求得AB的长,比较大小即可求得需要爬行的最短路程.
将长方体沿CF、FG、GH剪开,向右翻折,使面FCHG和面ADCH在同一个平面内,
连接AB,如图1,
由题意可得:BD=BC+CD=5+10=15cm,AD=CH=15cm,
在Rt△ABD中,根据勾股定理得:![]()
将长方体沿DE、EF、FC剪开,向上翻折,使面DEFC和面ADCH在同一个平面内,
连接AB,如图2,
由题意得:BH=BC+CH=5+15=20cm,AH=10cm,
在Rt△ABH中,根据勾股定理得:![]()
则需要爬行的最短距离是15![]() cm.
cm.
连接AB,如图3,
由题意可得:BB′=B′E+BE=15+10=25cm,AB′=BC=5cm,
在Rt△AB′B中,根据勾股定理得:![]()
∵![]()
∴则需要爬行的最短距离是![]()


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:
【题目】如图,杭州某化工厂与A,B两地有公路,铁路相连.这家工厂从A地购买一批每吨1000元的原料运回工厂,制成每吨8000元的产品运到B地.已知公路运价为1.4元/(吨千米),铁路运价为1.1元/(吨千米),且这两次运输共支出公路运输费14000元,铁路运输费89100元,求:
(1)该工厂从A地购买了多少吨原料?制成运往B地的产品多少吨?
(2)这批产品的销售款比原料费与运输费的和多多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
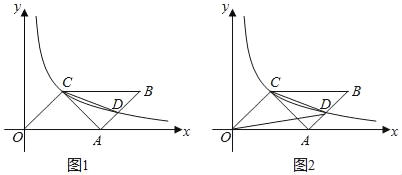
【题目】如图1,在平面直角坐标系中,OABC的一个顶点与坐标原点重合,OA边落在x轴上,且OA=4,OC=2![]() ,∠COA=45°.反比例函数y=
,∠COA=45°.反比例函数y=![]() (k>0,x>0)的图象经过点C,与AB交于点D,连接AC,CD.
(k>0,x>0)的图象经过点C,与AB交于点D,连接AC,CD.
(1)试求反比例函数的解析式;
(2)求证:CD平分∠ACB;
(3)如图2,连接OD,在反比例的函数图象上是否存在一点P,使得S△POC=![]() S△COD?如果存在,请直接写出点P的坐标.如果不存在,请说明理由.
S△COD?如果存在,请直接写出点P的坐标.如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c的顶点为D(﹣1,2),与x轴的一个交点A在点(﹣3,0)和
(﹣2,0)之间,其部分图象如下图,则以下结论:①b2﹣4ac<0;②a+b+c<0;③c﹣a=2;④方程ax2+bx+c﹣2=0有两个相等的实数根.其中正确结论的个数为( )

A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明坐在堤边A处垂钓,河堤AC与水平面的夹角为30°,AC的长为![]() 米,钓竿AO与水平线的夹角为60°,其长为3米,若AO与钓鱼线OB的夹角为60°,求浮漂B与河堤下端C之间的距离.
米,钓竿AO与水平线的夹角为60°,其长为3米,若AO与钓鱼线OB的夹角为60°,求浮漂B与河堤下端C之间的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表给出了1班6名学生的身高情况与全班平均身高的差值(单位:厘米)
学生 | A | B | C | D | E | F |
身高 | 157 | 162 | 159 | 152 | 163 | 164 |
身高与全班平均身高的差值 | -3 | +2 | -1 | a | +3 | b |
(1)列式计算表中数据a和b
(2)这6名学生的平均身高与全班学生的平均身高相比,在数值上有什么关系?(通过计算回答)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂一周计划每日生产自行车100辆,由于工人实行轮休,每日上班人数不一定相等,实际每日生产量与计划量相比情况如下表(以计划量为标准,增加的车辆数记为正数,减少的车辆数记为负数):

(1)生产量最多的一天比生产量最少的一天多生产多少辆?
(2)本周总的生产量是多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是一个由1~28的连续整数排成的“数阵”.如图2,用2×2的方框围住了其中的四个数,如果围住的这四个数中的某三个数的和是27,那么这三个数是a,b,c,d中的_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com