
ЁОЬтФПЁПзлКЯЬНОПЃКШчЭМ1ЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌХзЮяЯпy=Љ![]() +bx+8гыxжсНЛгкЕуAЃЈЉ6ЃЌ0ЃЉКЭЕуBЃЈЕуAдкЕуBзѓВрЃЉЃЌгыyжсНЛгкЕуCЃЌЕуPЮЊЯпЖЮAOЩЯЕФвЛИіЖЏЕуЃЌЙ§ЕуPзїxжсЕФДЙЯпlгыХзЮяЯпНЛгкЕуEЃЌСЌНгAEЁЂECЃЎ
+bx+8гыxжсНЛгкЕуAЃЈЉ6ЃЌ0ЃЉКЭЕуBЃЈЕуAдкЕуBзѓВрЃЉЃЌгыyжсНЛгкЕуCЃЌЕуPЮЊЯпЖЮAOЩЯЕФвЛИіЖЏЕуЃЌЙ§ЕуPзїxжсЕФДЙЯпlгыХзЮяЯпНЛгкЕуEЃЌСЌНгAEЁЂECЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФБэДяЪНМАЕуCЕФзјБъЃЛ
ЃЈ2ЃЉСЌНгACНЛжБЯпlгкЕуDЃЌдђдкЕуPдЫЖЏЙ§ГЬжаЃЌЕБЕуDЮЊEPжаЕуЪБЃЌSЁїADPЃКSЁїCDE=ЁЁ ЁЁЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌЕБECЁЮxжсЪБЃЌЕуPЭЃжЙдЫЖЏЃЌДЫЪБЃЌдкХзЮяЯпЩЯЪЧЗёДцдкЕуGЃЌЪЙЕУвдЕуAЁЂEЁЂGЮЊЖЅЕуЕФШ§НЧаЮЪЧжБНЧШ§НЧаЮЃПШєДцдкЃЌЧыЧѓГіЕуGЕФзјБъЃЌШєВЛДцдкЃЌЫЕУїРэгЩЃЎ

ЁОД№АИЁПЃЈ1ЃЉCЃЈ0ЃЌ8ЃЉЃЈ2ЃЉ1ЃК2ЃЈ3ЃЉДцдкЕуGЪЙЕУвдЕуAЃЌEЃЌGЮЊЖЅЕуЕФШ§НЧаЮЮЊжБНЧШ§НЧаЮЃЌЗћКЯЬѕМўЕФGЕуЕФзјБъЮЊGЃЈ![]() ЃЌ
ЃЌ ![]() ЃЉЛђGЃЈ
ЃЉЛђGЃЈ![]() ЃЌЉ
ЃЌЉ![]() ЃЉЃЌ
ЃЉЃЌ
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉгУД§ЖЈЯЕЪ§ЗЈЧѓГіХзЮяЯпНтЮіЪНЃЌСю![]() ЧѓГі
ЧѓГі![]() жсНЛЕузјБъЃЛ
жсНЛЕузјБъЃЛ
ЃЈ2ЃЉЯШШЗЖЈГіжБЯп![]() НтЮіЪНЮЊ
НтЮіЪНЮЊ![]() ЩшГіЕуEЕФзјБъЃЌБэЪОГіЕу
ЩшГіЕуEЕФзјБъЃЌБэЪОГіЕу![]() ЖјЕуDдкжБЯпACЩЯЃЌСаГіЗНГЬ
ЖјЕуDдкжБЯпACЩЯЃЌСаГіЗНГЬ![]()
ЧѓГі![]() ЃЌДгЖјЕУГіНсТлЃЛ
ЃЌДгЖјЕУГіНсТлЃЛ
ЃЈ3ЃЉЯШЧѓГіЕу![]() ЕФзјБъЃЌдйЗжСНжжЧщПіМЦЫуЂёЁЂЕБ
ЕФзјБъЃЌдйЗжСНжжЧщПіМЦЫуЂёЁЂЕБ![]() ЪБЃЌХаЖЯГіЁїEMGЁзЁїAPEЃЌЕУГіБШР§ЪНЧѓНтМДПЩЃЌЂђЁЂЕБ
ЪБЃЌХаЖЯГіЁїEMGЁзЁїAPEЃЌЕУГіБШР§ЪНЧѓНтМДПЩЃЌЂђЁЂЕБ![]() ЪБЃЌХаЖЯГіЁїGNAЁзЁїAPEЃЌЕУЕНБШР§ЪНМЦЫуЃЎ
ЪБЃЌХаЖЯГіЁїGNAЁзЁїAPEЃЌЕУЕНБШР§ЪНМЦЫуЃЎ
ЪдЬтНтЮіЃК(1)ЁпЕуA(6,0)дкХзЮяЯп![]() ЩЯЃЌ
ЩЯЃЌ
Ёр![]()
![]()
Ёр![]()
Сюx=0ЃЌy=8ЃЌ
ЁрC(0,8)
(2)Щш![]()
ЁрP(m,0)ЃЌ
ЁпЕуDЮЊEPжаЕуЃЌ
ЁрDP=DE, ![]()
ЁпA(6,0),C(0,8)ЃЌ
ЁржБЯпACНтЮіЪНЮЊ![]()
ЁпЕуDдкжБЯпACЩЯЃЌ
Ёр![]()
Ёрm=6(
ЁрP(4,0)
ЁрAP=2ЃЌOP=4ЃЌ
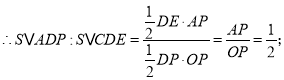
ЙЪД№АИЮЊ1:2
(3)ДцдкЕуGЪЙЕУвдЕуAЃЌEЃЌGЮЊЖЅЕуЕФШ§НЧаЮЮЊжБНЧШ§НЧаЮЃЌ
СЌНгEGЃЌAGЃЌзїGMЁЭlЃЌGNЁЭxжсЃЌ
ЁпECЁЮxжсЃЌ
ЁрEP=CO=8ЃЌ
Абy=8ДњШы![]()
Ёр![]()
Ёрx=0(Щс)ЃЌЛђx=2ЃЌ
ЁрP(2,0)ЃЌ
ЁрAP=AOPO=4ЃЌ
ЂёЁЂШчЭМ1ЃЌ
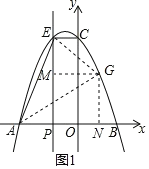
ЕБ![]() ЪБЃЌ
ЪБЃЌ
Ёр![]()
Ёп![]()
ЁрЁЯMEG=ЁЯEAPЃЌ
Ёп![]()
ЁрЁїEMGЁзЁїAPEЃЌ
Ёр![]()
ЩшЕу![]()
![]()
Ёр![]()
MG=PN=PO+ON=2+mЃЌ
![]()
Ёр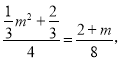 Ёрm=2(Щс)Лђ
Ёрm=2(Щс)Лђ![]()
Ёр![]()
ЂђЁЂШчЭМ2ЃЌ
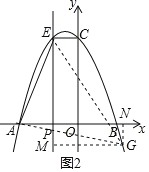
ЕБ![]() ЪБЃЌ
ЪБЃЌ
Ёр![]()
Ёп![]()
ЁрЁЯNAG=ЁЯAEPЃЌ
Ёп![]()
ЁрЁїGNAЁзЁїAPEЃЌ
Ёр![]()
ЩшЕу![]()
![]()
ЁрAN=AO+ON=6+nЃЌ
Ёп![]()

Ёрn=6(Щс),Лђ![]()
Ёр![]()
ЗћКЯЬѕМўЕФGЕуЕФзјБъЮЊ![]() Лђ
Лђ![]()



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЙлВьЯТСаСНИіЕШЪНЃК2![]() =2ЁС
=2ЁС![]() +1ЃЌ5
+1ЃЌ5![]() =5ЁС
=5ЁС![]() +1ЃЌИјГіЖЈвхШчЯТЃКЮвУЧГЦЪЙЕШЪНabЃНabЃЋ1ЕФГЩСЂЕФвЛЖдгаРэЪ§aЃЌbЮЊЁАЙВЩњгаРэЪ§ЖдЁБЃЌМЧЮЊЃЈaЃЌbЃЉЃЌШчЃКЪ§ЖдЃЈ2ЃЌ
+1ЃЌИјГіЖЈвхШчЯТЃКЮвУЧГЦЪЙЕШЪНabЃНabЃЋ1ЕФГЩСЂЕФвЛЖдгаРэЪ§aЃЌbЮЊЁАЙВЩњгаРэЪ§ЖдЁБЃЌМЧЮЊЃЈaЃЌbЃЉЃЌШчЃКЪ§ЖдЃЈ2ЃЌ![]() ЃЉЃЌЃЈ5ЃЌ
ЃЉЃЌЃЈ5ЃЌ![]() ЃЉЃЌЖМЪЧЁАЙВЩњгаРэЪ§ЖдЁБЃЎ
ЃЉЃЌЖМЪЧЁАЙВЩњгаРэЪ§ЖдЁБЃЎ
(1)ХаЖЯЪ§Жд(2,1),(3,![]() )ЪЧВЛЪЧЁАЙВЩњгаРэЪ§ЖдЁБЃЌаДГіЙ§ГЬЃЛ
)ЪЧВЛЪЧЁАЙВЩњгаРэЪ§ЖдЁБЃЌаДГіЙ§ГЬЃЛ
(2)Шє(a,3)ЪЧЁАЙВЩњгаРэЪ§ЖдЁБЃЌЧѓaЕФжЕЃЛ
(3)Шє(m,n)ЪЧЁАЙВЩњгаРэЪ§ЖдЁБ,дђ(n,m)ЁАЙВЩњгаРэЪ§ЖдЁБ(ЬюЁАЪЧЁБЛђЁАВЛЪЧЁБ)ЃЛЫЕУїРэгЩЃЛ
(4)ЧыдйаДГівЛЖдЗћКЯЬѕМўЕФЁАЙВЩњгаРэЪ§ЖдЁБЮЊ(зЂвтЃКВЛФмгыЬтФПжавбгаЕФЁАЙВЩњгаРэЪ§ЖдЁБжиИД).
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌЁЯC=90ЁуЃЌMЪЧABЕФжаЕуЃЌЖЏЕуPДгЕуAГіЗЂЃЌбиACЗНЯђдШЫйдЫЖЏЕНжеЕуCЃЌЖЏЕуQДгЕуCГіЗЂЃЌбиCBЗНЯђдШЫйдЫЖЏЕНжеЕуBЃЎвбжЊPЃЌQСНЕуЭЌЪБГіЗЂЃЌВЂЭЌЪБЕНДяжеЕуЃЌСЌНгMPЃЌMQЃЌPQЃЎдкећИідЫЖЏЙ§ГЬжаЃЌЁїMPQЕФУцЛ§ДѓаЁБфЛЏЧщПіЪЧЃЈЁЁЁЁЃЉ

A. вЛжБдіДѓ B. вЛжБМѕаЁ C. ЯШМѕаЁКѓдіДѓ D. ЯШдіДѓКѓМѕЩй
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌаЁУїзјдкЕЬБпAДІДЙЕіЃЌКгЕЬACгыЫЎЦНУцЕФМаНЧЮЊ30ЁуЃЌACЕФГЄЮЊ![]() УзЃЌЕіИЭAOгыЫЎЦНЯпЕФМаНЧЮЊ60ЁуЃЌЦфГЄЮЊ3УзЃЌШєAOгыЕігуЯпOBЕФМаНЧЮЊ60ЁуЃЌЧѓИЁЦЏBгыКгЕЬЯТЖЫCжЎМфЕФОрРыЃЎ
УзЃЌЕіИЭAOгыЫЎЦНЯпЕФМаНЧЮЊ60ЁуЃЌЦфГЄЮЊ3УзЃЌШєAOгыЕігуЯпOBЕФМаНЧЮЊ60ЁуЃЌЧѓИЁЦЏBгыКгЕЬЯТЖЫCжЎМфЕФОрРыЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМAдкЪ§жсЩЯЖдгІЕФЪ§ЮЊ-2.
(1)ЕуBдкЕуAгвБпОрРыAЕу4ИіЕЅЮЛГЄЖШЃЌдђЕуBЫљЖдгІЕФЪ§ЪЧ_____.
(2)дк(1)ЕФЬѕМўЯТЃЌЕуAвдУПУы2ИіЕЅЮЛГЄЖШбиЪ§жсЯђзѓдЫЖЏЃЌЕуBвдУПУы3ИіЕЅЮЛГЄЖШбиЪ§жсЯђгвдЫЖЏ.ЯжСНЕуЭЌЪБдЫЖЏ,ЕБЕуAдЫЖЏЕН-6ЕФЕуДІЪБЃЌЧѓAЁЂBСНЕуМфЕФОрРы.
(3)дк(2)ЕФЬѕМўЯТЃЌЯжAЕуОВжЙВЛЖЏЃЌBЕувддЫйбиЪ§жсЯђзѓдЫЖЏЃЌОЙ§ЖрГЄЪБМфAЁЂBСНЕуЯрОр4ИіЕЅЮЛГЄЖШ.
![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТБэИјГіСЫ1Ар6УћбЇЩњЕФЩэИпЧщПігыШЋАрЦНОљЩэИпЕФВюжЕЃЈЕЅЮЛЃКРхУзЃЉ
бЇЩњ | A | B | C | D | E | F |
ЩэИп | 157 | 162 | 159 | 152 | 163 | 164 |
ЩэИпгыШЋАрЦНОљЩэИпЕФВюжЕ | -3 | +2 | -1 | a | +3 | b |
ЃЈ1ЃЉСаЪНМЦЫуБэжаЪ§ОнaКЭb
ЃЈ2ЃЉет6УћбЇЩњЕФЦНОљЩэИпгыШЋАрбЇЩњЕФЦНОљЩэИпЯрБШЃЌдкЪ§жЕЩЯгаЪВУДЙиЯЕЃПЃЈЭЈЙ§МЦЫуЛиД№ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
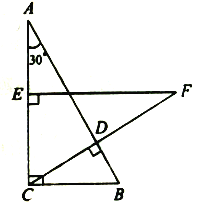
ЁОЬтФПЁПШчЭМЃЌдкRtЁїABCжаЃЌЁЯACB=90ЁуЃЌЁЯA=30ЁуЃЌBC=3cmЃЌCDЁЭABЃЌдкACЩЯШЁвЛЕуEЃЌЪЙEC=BCЃЌЙ§ЕуEзїEFЁЭACНЛCDЕФбгГЄЯпгкЕуFЃЌЧѓEFКЭAEЕФГЄ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПДг2018Фъ4дТ1ШеЦ№ЯУУХЪаЪЕаааТЕФздРДЫЎЪеЗбНзЬнЫЎМлЪеЗбБъзМШчЯТБэ.

БИзЂ:1.УПдТОгУёгУЫЎНЩЗбАќРЈЪЕМЪгУЫЎЕФЫЎЗбКЭЮлЫЎДІРэЗбСНВПЗж.2.вдЩЯБэжаЕФМлИёОљВЛАќРЈ1дЊ/ЖжЕФЮлЫЎДІРэЗб.
(1)ФГгУЛЇ12дТЗнгУЫЎСПЮЊ20Жж,дђИУгУЛЇ12дТЗнгІНЩЫЎЗбЪЧЖрЩй?
(2)ШєФГгУЛЇЕФдТгУЫЎСПЮЊmЖж,ЧыгУКЌmЕФЪНзгБэЪОИУгУЛЇдТЫљНЩЫЎЗб.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
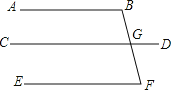
ЁОЬтФПЁПШчЭМЃКвбжЊЁЯBЃНЁЯBGDЃЌЁЯDGFЃНЁЯFЃЌЧѓжЄЃКЁЯB+ЁЯFЃН180ЁуЃЎ
ЧыФуШЯецЭъГЩЯТУцЕФЬюПеЃЎ
жЄУїЃКЁпЁЯBЃНЁЯBGD ЃЈ вбжЊ ЃЉ
ЁрABЁЮCD ЃЈЁЁ ЁЁЃЉ
ЁпЁЯDGFЃНЁЯFЃЛЃЈ вбжЊ ЃЉ
ЁрCDЁЮEF ЃЈЁЁ ЁЁ ЃЉ
ЁрABЁЮEF ЃЈЁЁ ЁЁ ЃЉ
ЁрЁЯB+ЁЯFЃН180ЁуЃЈЁЁ ЁЁ ЃЉЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com