
【题目】(1)如图①,在平行四边形ABCD中,AC、BD交于点O,过点O作直线EF分别交AD、BC于点E、F,
求证:OE=OF.
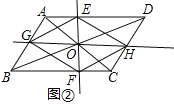
(2)在图①中,过点O作直线GH分别交AB、CD于点G、H,且满足GH⊥EF,连结EG、GF、FH、HE.如图②,试判断四边形EGFH的形状,并说明理由;
(3)在(2)的条件下,
若平行四边形ABCD变为矩形时,四边形EGFH是 ;
若平行四边形ABCD变为菱形时,四边形EGFH是 ;
若平行四边形ABCD变为正方形时,四边形EGFH是 .
【答案】(1)见解析(2)见解析(3)菱形;菱形;正方形
【解析】
试题分析:(1)由于平行四边形对角线的交点是它的对称中心,即可得出OE=OF、OG=OH;根据对角线互相平分的四边形是平行四边形即可判断出EGFH的性质;
(2)当EF⊥GH时,平行四边形EGFH的对角线互相垂直平分,故四边形EGFH是菱形;
(3)若平行四边形ABCD变为矩形,即AC=BD时,对四边形EGFH的形状不会产生影响,故结论同(2);
若平行四边形ABCD变为菱形,即AC⊥BD时,对四边形EGFH的形状不会产生影响,故结论同(2);
当四边形ABCD是正方形,则对角线相等且互相垂直平分;可通过证△BOG≌△COF,得OG=OF,从而证得菱形的对角线相等,根据对角线相等的菱形是正方形即可判断出EGFH的形状.
(1)证明:∵四边形ABCD是平行四边形,
∴AO=CO,AD∥BC,
∴∠DAC=∠BCA,
在△AOE和△COF中,
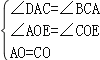 ,
,
∴△AOE≌△COF(AAS),
∴EO=FO;
(2)解:四边形EGFH是菱形;
理由:如图②:
由(1)可知,OE=OF,
同理可得:OG=OH,
∴四边形EGFH是平行四边形,
又∵EF⊥GH,
∴四边形EGFH是菱形;
(3)解:若平行四边形ABCD变为矩形时,四边形EGFH是菱形;
理由:由(2)知四边形EGFH是菱形,
当AC=BD时,对四边形EGFH的形状不会产生影响;
故答案为:菱形;
若平行四边形ABCD变为菱形时,四边形EGFH是菱形;
理由:由(2)知四边形EGFH是菱形,
当AC⊥BD时,对四边形EGFH的形状不会产生影响;
故答案为:菱形;
若平行四边形ABCD变为正方形时,四边形EGFH是四边形EGFH是正方形;
理由:∵四边形ABCD是正方形,
∴∠BOC=90°,∠GBO=∠FCO=45°,OB=OC;
∵EF⊥GH,
∴∠GOF=90°;
∠BOG+∠BOF=∠COF+∠BOF=90°
∴∠BOG=∠COF;
在△BOG和△COF中
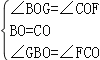 ,
,
∴△BOG≌△COF(ASA);
∴OG=OF,
同理可得:EO=OH,
∴GH=EF;
由(3)知四边形EGFH是菱形,
又EF=GH,
∴四边形EGFH是正方形.
故答案为:正方形.


科目:初中数学 来源: 题型:
【题目】如图①,南京中山陵的台阶拾级而上被分成坡度不等的两部分.图②是台阶的侧面图,若斜坡BC长为120m,在C处看B处的仰角为25°;斜坡AB长70m,在A处看B处的俯角为50°,试求出陵墓的垂直高度AE的长.
(参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.19,sin25°≈0.42,cos25°≈0.91,tan25°≈0.47)

考点:解直角三角形的应用-仰角俯角问题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=kx+b与x轴交于点A,与y轴交于点B,且四边形AOBC是矩形,BC=6,矩形AOBC的面积为18.

(1)求线段OC的长.
(2)求直线AB的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一位“粗心”的同学在做加减运算时,将“-100”错写成“+100”进行运算,这样他得到的结果比正确答案( )
A. 少100 B. 少200 C. 多100 D. 多200
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线y=ax+b(a≠0)经过第一,二,四象限,那么直线y=bx-a一定不经过( )
A. 第一象限
B. 第二象限
C. 第三象限
D. 第四象限
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(请在括号里注明重要的推理依据)
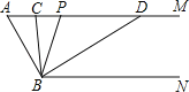
如图,已知AM∥BN,∠A=60°.点P是射线AM上一动点(与点A不重合),BC、BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.
(1)求∠CBD的度数;
(2)当点P运动时,∠APB与∠ADB之间的数量关系是否随之发生变化?若不变化,请写出它们之间的关系,并说明理由;若变化,请写出变化规律.
(3)当点P运动到使∠ACB=∠ABD时,∠ABC的度数是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知P(﹣3,m)和 Q(1,m)是抛物线y=x2+bx﹣3上的两点.

(1)求b的值;
(2)将抛物线y=x2+bx﹣3的图象向上平移k(是正整数)个单位,使平移后的图象与x轴无交点,求k的最小值;
(3)将抛物线y=x2+bx﹣3的图象在x轴下方的部分沿x轴翻折,图象的其余部分保持不变,得到一个新的图象,请你结合新图象回答:当直线y=x+n与这个新图象有两个公共点时,求n的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com