
【题目】如图 1,直线 m 与直线 n 垂直相交于点 O ,点 A 在直线 m 上运动,点 B 在直线 n 上运动, AC 、 BC 分别是BAO 和ABO 的角平分线.
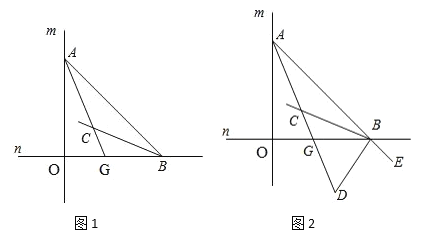
(1)求ACB 的大小;
(2)如 图 2,若 BD 是AOB 的外角OBE 的角平分线,BD 与 AC 相交于点 D ,点 A 、B 在运动的过程中,ADB的大小是否会发生变化?若发生变化,请说明理由,若不发生变化,试求出其值.
【答案】(1)135°,(2)45°.
【解析】
(1)根据三角形的内角和得到∠OAB+∠OBA=90°,再根据AC 、 BC 分别是BAO 和ABO 的角平分线得到∠CAB+∠CBA=45°,再利用三角形的内角和即可求解∠ACB的度数;
(2)根据BC是ABO 的角平分线,BD是OBE 的角平分线得到∠DBC=90°,由(1)得到∠BCD=45°,故可求出∠ADB的度数.
(1)AO⊥BO,∴∠OAB+∠OBA=90°
∵AC 、 BC 分别是BAO 和ABO 的角平分线
∴∠CAB+∠CBA=![]() ∠OAB +
∠OAB +![]() ∠OBA =
∠OBA =![]() (∠OAB+∠OBA)=45°
(∠OAB+∠OBA)=45°
∴∠ACB=180°-(∠CAB+∠CBA)=135°,
(2)不变,∠ADB=45°,
理由如下:
∵BC是ABO 的角平分线,BD是OBE 的角平分线
∴∠DBC=∠DBG+∠GBC=![]() ∠EBG +
∠EBG +![]() ∠OBA=
∠OBA=![]() (∠EBG+∠OBA)=90°,
(∠EBG+∠OBA)=90°,
又∠BCD=180°-ACB =45°
∴∠ADB=180°-∠DBC-∠BCD=45°.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】某商城销售A,B两种自行车.A型自行车售价为2 100元/辆,B型自行车售价为1 750元/辆,每辆A型自行车的进价比每辆B型自行车的进价多400元,商城用80 000元购进A型自行车的数量与用64 000元购进B型自行车的数量相等.
(1)求每辆A,B两种自行车的进价分别是多少?
(2)现在商城准备一次购进这两种自行车共100辆,设购进A型自行车m辆,这100辆自行车的销售总利润为y元,要求购进B型自行车数量不超过A型自行车数量的2倍,总利润不低于13 000元,求获利最大的方案以及最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了让学生能更加了解温州历史,某校组织七年级师生共480人参观温州博物馆.学校向租车公司租赁A、B两种车型接送师生往返,若租用A型车3辆,B型车6辆,则空余15个座位;若租用A型车5辆,B型车4辆,则15人没座位.
(1)求A、B两种车型各有多少个座位;
(2)若A型车日租金为350元,B型车日租金为400元,且租车公司最多能提供7辆B型车,应怎样租车能使座位恰好坐满且租金最少,并求出最少租金.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AE=AC,AB=AD,∠EAB=∠CAD.
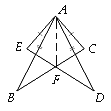
(1)BC与DE相等吗?说明理由.
(2)若BC与DE相交于点F,EF=CF.连接AF,∠BAF与∠DAF相等吗?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,已知一次函数
中,已知一次函数![]() =
=![]() 的图象经过点A(1,0),与反比例函数
的图象经过点A(1,0),与反比例函数![]() =
=![]() (
(![]() >0)的图象相交于点B(m,1).
>0)的图象相交于点B(m,1).
(1)求m的值和一次函数的解析式;
(2)结合图象直接写出:当![]() >0时,不等式
>0时,不等式![]() >
>![]() 的解集.
的解集.

查看答案和解析>>
科目:初中数学 来源: 题型:
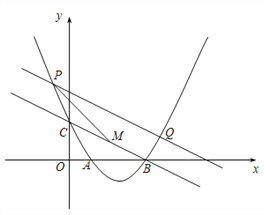
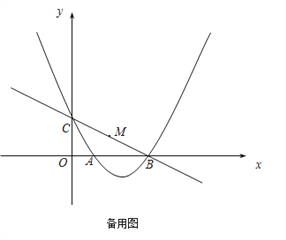
【题目】如图,在平面直角坐标系中,抛物线![]() 与x轴交于A,B两点(点A在点B的左边),与y轴交于点C.点P为抛物线上一动点,过点P作PQ∥BC交抛物线于点Q,P、Q两点之间的距离为m.
与x轴交于A,B两点(点A在点B的左边),与y轴交于点C.点P为抛物线上一动点,过点P作PQ∥BC交抛物线于点Q,P、Q两点之间的距离为m.
(1)求直线BC的解析式;
(2)取线段BC的中点M,连接PM.当m最小时,判断以点P、O、M、B为顶点的四边形是什么特殊的平行四边形,并说明理由;
(3)设N为y轴上一点,在(2)的基础上,当∠OBN=2∠OBP时,求点N的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O中,直径CD⊥弦AB于M,AE⊥BD于E,交CD于N,连AC
(1)求证:AC=AN;
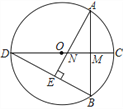
(2)若OM∶OC=3∶5,AB=5,求⊙O的半径;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国魏晋时期数学家刘徽编撰的最早一部测量数学著作《海岛算经》中有一题:今有望海岛,立两表齐高三丈,前后相去千步,令后表与前表参相直.从前表却行一百二十三步,人目着地,取望岛峰,与表末参合.从后表却行一百二十七步,人目着地,取望岛峰,亦与表末参合.问岛高几何?

译文:今要测量海岛上一座山峰AH的高度,在B处和D处树立标杆BC和DE,标杆的高都是3丈,B和D两处相隔1000步(1丈=10尺,1步=6尺),并且AH,CB和DE在同一平面内.从标杆BC后退123步的F处可以看到顶峰A和标杆顶端C在同一直线上;从标杆ED后退127步的G处可以看到顶峰A和标杆顶端E在同一直线上.则山峰AH的高度是_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在边长为1的小正方形网格中,△AOB的顶点均在格点上.
(1)B点关于y轴的对称点坐标为 ;
(2)将△AOB向左平移3个单位长度得到△A1O1B1,请画出△A1O1B1;
(3)在(2)的条件下,A1的坐标为 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com