
 如图,在平面直角坐标系中,直线y=-3x+3与x轴、y轴分别交于A、B两点,以AB为边在第一象限作正方形ABCD,顶点D恰好落在双曲线y=$\frac{y}{x}$.若将正方形沿x轴向左平移b个单位长度后,点C恰好落在该双曲线上,则b的值为( )
如图,在平面直角坐标系中,直线y=-3x+3与x轴、y轴分别交于A、B两点,以AB为边在第一象限作正方形ABCD,顶点D恰好落在双曲线y=$\frac{y}{x}$.若将正方形沿x轴向左平移b个单位长度后,点C恰好落在该双曲线上,则b的值为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 作DE⊥x轴于E,CF⊥y轴于F,如图,先根据坐标轴上点的坐标特征得到B(0,3),A(1,0),再证明△AOB≌△DEA得到AE=OB=3,DE=OA=1,则D(4,1),同样方法可得C(3,4),接着根据反比例函数图象上点的坐标特征确定k=4,则反比例函数解析式为y=$\frac{4}{x}$,然后计算当y=4时所对应的自变量,从而可确定b的值.
解答 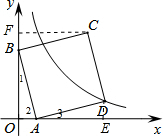 解:作DE⊥x轴于E,CF⊥y轴于F,如图,
解:作DE⊥x轴于E,CF⊥y轴于F,如图,
当x=0时,y=-3x+3=3,则B(0,3);当y=0时,-3x+3=0,解得x=1,则A(1,0),
∵四边形ABCD为正方形,
∴AB=AD,∠BAD=90°,
∴∠2+∠3=90°,
而∠1+∠3=90°,
∴∠1=∠3,
在△AOB和△DEA中
$\left\{\begin{array}{l}{∠AOB=∠DEA}\\{∠1=∠2}\\{AB=DA}\end{array}\right.$,
∴△AOB≌△DEA,
∴AE=OB=3,DE=OA=1,
∴D(4,1),
同样方法可得△AOB≌△BFC,
∴CF=OB=3,BF=OA=1,
∴C(3,4),
而顶点D落在双曲线y=$\frac{y}{x}$,
∴k=4×1=4,
∴反比例函数解析式为y=$\frac{4}{x}$,
当y=4时,$\frac{4}{x}$=4,解得x=1,
∴C点向左平移2个单位恰好落在该双曲线上,
即b=2.
故选B.
点评 本题考查了反比例函数图象上点的坐标特征:反比例函数y=$\frac{k}{x}$(k为常数,k≠0)的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.也考查了正方形的性质和平移变换.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
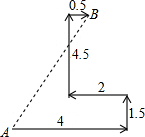 中国机器人创意大赛于2014年7月15日在哈尔滨开幕.如图是一参赛队员设计的机器人比赛时行走的路径,机器人从A处先往东走4m,又往北走1.5m,遇到障碍后又往西走2m,再转向北走4.5m处往东一拐,仅走0.5m就到达了B.问机器人从点A到点B之间的距离是多少?
中国机器人创意大赛于2014年7月15日在哈尔滨开幕.如图是一参赛队员设计的机器人比赛时行走的路径,机器人从A处先往东走4m,又往北走1.5m,遇到障碍后又往西走2m,再转向北走4.5m处往东一拐,仅走0.5m就到达了B.问机器人从点A到点B之间的距离是多少?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | k≤2 | B. | k<1 | C. | k≥2 | D. | 1≤k<2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
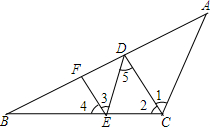 已知:如图,AC∥DE,DC∥EF,CD平分∠BCD.求证:EF平分∠BED.
已知:如图,AC∥DE,DC∥EF,CD平分∠BCD.求证:EF平分∠BED.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
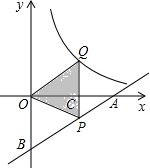 如图,一次函数y=$\frac{1}{2}$x-2的图象分别交x轴、y轴于A、B,P为AB上一点且PC为△AOB的中位线,PC的延长线交反比例函数y=$\frac{5}{x}$(x>0)的图象于Q,则S△OQP=$\frac{7}{2}$.
如图,一次函数y=$\frac{1}{2}$x-2的图象分别交x轴、y轴于A、B,P为AB上一点且PC为△AOB的中位线,PC的延长线交反比例函数y=$\frac{5}{x}$(x>0)的图象于Q,则S△OQP=$\frac{7}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com