
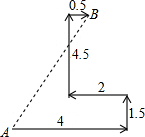
 中国机器人创意大赛于2014年7月15日在哈尔滨开幕.如图是一参赛队员设计的机器人比赛时行走的路径,机器人从A处先往东走4m,又往北走1.5m,遇到障碍后又往西走2m,再转向北走4.5m处往东一拐,仅走0.5m就到达了B.问机器人从点A到点B之间的距离是多少?
中国机器人创意大赛于2014年7月15日在哈尔滨开幕.如图是一参赛队员设计的机器人比赛时行走的路径,机器人从A处先往东走4m,又往北走1.5m,遇到障碍后又往西走2m,再转向北走4.5m处往东一拐,仅走0.5m就到达了B.问机器人从点A到点B之间的距离是多少?  阶梯计算系列答案
阶梯计算系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
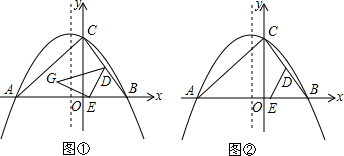
 如图,在平面直角坐标系中,直线y=-3x+3与x轴、y轴分别交于A、B两点,以AB为边在第一象限作正方形ABCD,顶点D恰好落在双曲线y=$\frac{y}{x}$.若将正方形沿x轴向左平移b个单位长度后,点C恰好落在该双曲线上,则b的值为( )
如图,在平面直角坐标系中,直线y=-3x+3与x轴、y轴分别交于A、B两点,以AB为边在第一象限作正方形ABCD,顶点D恰好落在双曲线y=$\frac{y}{x}$.若将正方形沿x轴向左平移b个单位长度后,点C恰好落在该双曲线上,则b的值为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com