
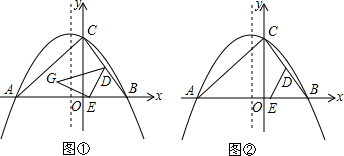
���� ��1������������y=ax2+bx+8������A��-6��0����B��4��0����Ӧ�ô���ϵ��������������ߵĽ���ʽ���ɣ�
��2��������DM�������ߵĶԳ����ڵ�M����G�������Ϊ��-1��n�������ݷ��۵����ʣ��ɵ�BD=DG��Ȼ��ֱ������D����M��������Ƕ��٣��Լ�BC��BD��ֵ���Ƕ��٣������Rt��GDM�У����ݹ��ɶ��������n��ֵ���������G������꣮
��3���������⣬������������ٵ�CD��EF���ҵ�E��x���������ʱ���ڵ�CD��EF���ҵ�E��x��ĸ�����ʱ���۵�CE��DFʱ��Ȼ�����ƽ���ı��ε����ʣ������F��������Ƕ��ټ��ɣ�
��� �⣺��1����������y=ax2+bx+8������A��-6��0����B��4��0����
��$\left\{\begin{array}{l}{36a-6b+8=0}\\{16a+4b+8=0}\end{array}\right.$
���$\left\{\begin{array}{l}{a=-\frac{1}{3}}\\{b=-\frac{2}{3}}\end{array}\right.$
�������ߵĽ���ʽ�ǣ�y=-$\frac{1}{3}$x2-$\frac{2}{3}$x+8��
��2����ͼ�٣���DM�������ߵĶԳ����ڵ�M��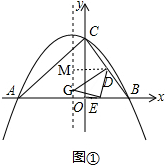 ��
��
��G���������-1��n����
�ɷ��۵����ʣ��ɵ�BD=DG��
��B��4��0����C��0��8������DΪBC���е㣬
���D�������ǣ�2��4����
���M�������ǣ�-1��4����DM=2-��-1��=3��
��B��4��0����C��0��8����
��BC=$\sqrt{{4}^{2}{+8}^{2}}$=4$\sqrt{5}$��
��$BD=2\sqrt{5}$��
��Rt��GDM��
32+��4-n��2=20��
���n=4��$\sqrt{11}$��
��G���������-1��4+$\sqrt{11}$����-1��4-$\sqrt{11}$����
��3��������y=ax2+bx+8�ĶԳ����ϴ��ڵ�F��ʹ����C��D��E��FΪ������ı���Ϊƽ���ı��Σ�
�ٵ�CD��EF���ҵ�E��x���������ʱ����ͼ��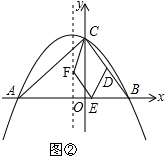 ��
��
�ɣ�2�����ɵõ�D�������ǣ�2��4����
���E�������ǣ�c��0������F�������ǣ�-1��d����
��$\left\{\begin{array}{l}{\frac{0+c}{2}=\frac{-1+2}{2}}\\{\frac{8+0}{2}=\frac{d+4}{2}}\end{array}\right.$
���$\left\{\begin{array}{l}{c=1}\\{d=4}\end{array}\right.$
���F�������ǣ�-1��4������E�������ǣ�1��0����
�ڵ�CD��EF���ҵ�E��x��ĸ�����ʱ����ͼ�� ��
��
�ɣ�2�����ɵõ�D�������ǣ�2��4����
���E�������ǣ�c��0������F�������ǣ�-1��d����
��$\left\{\begin{array}{l}{\frac{0+��-1��}{2}=\frac{c+2}{2}}\\{\frac{8+d}{2}=\frac{0+4}{2}}\end{array}\right.$
���$\left\{\begin{array}{l}{c=-3}\\{d=-4}\end{array}\right.$
���F�������ǣ�-1��-4������E�������ǣ�-3��0����
�۵�CE��DFʱ����ͼ�ܣ�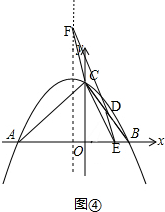 ��
��
�ɣ�2�����ɵõ�D�������ǣ�2��4����
���E�������ǣ�c��0������F�������ǣ�-1��d����
��$\left\{\begin{array}{l}{\frac{0+2}{2}=\frac{c+��-1��}{2}}\\{\frac{8+4}{2}=\frac{d+0}{2}}\end{array}\right.$
���$\left\{\begin{array}{l}{c=3}\\{d=12}\end{array}\right.$
���F�������ǣ�-1��12������E�������ǣ�3��0����
���ϣ��ɵ�
������y=ax2+bx+8�ĶԳ����ϴ��ڵ�F��ʹ����C��D��E��FΪ������ı���Ϊƽ���ı��Σ�
��F�������ǣ�-1��4������-1��-4����-1��12����
���� ��1��������Ҫ�����˶��κ����ۺ��⣬�����˷������������������˷�������˼���Ӧ�ã����������ν��˼���Ӧ�ã������˴���֪����ͼ���л�ȡ��Ϣ���������û�ȡ����Ϣ�����Ӧ�������������
��2�����������ƽ���ı��ε����ʺ�Ӧ�ã��Լ�����ϵ������������ʽ�ķ�����Ҫ�������գ�
��3�����������ֱ�������ε����ʺ�Ӧ�ã��Լ����ɶ�����Ӧ�ã�Ҫ�������գ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ֱ��l1��l2��l3��ֱ�������ε���������A��B��C�ֱ���l1��l2��l3�ϣ��ҡ�ABC=90�㣮����1=65�㣬���2=25�㣮
��ͼ��ֱ��l1��l2��l3��ֱ�������ε���������A��B��C�ֱ���l1��l2��l3�ϣ��ҡ�ABC=90�㣮����1=65�㣬���2=25�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
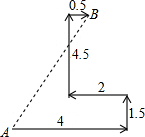 �й������˴��������2014��7��15���ڹ�������Ļ����ͼ��һ������Ա��ƵĻ����˱���ʱ���ߵ�·���������˴�A����������4m����������1.5m�������ϰ�����������2m����ת����4.5m������һ�գ�����0.5m�͵�����B���ʻ����˴ӵ�A����B֮��ľ����Ƕ��٣�
�й������˴��������2014��7��15���ڹ�������Ļ����ͼ��һ������Ա��ƵĻ����˱���ʱ���ߵ�·���������˴�A����������4m����������1.5m�������ϰ�����������2m����ת����4.5m������һ�գ�����0.5m�͵�����B���ʻ����˴ӵ�A����B֮��ľ����Ƕ��٣��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
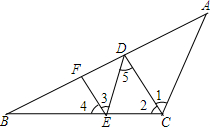 ��֪����ͼ��AC��DE��DC��EF��CDƽ�֡�BCD����֤��EFƽ�֡�BED��
��֪����ͼ��AC��DE��DC��EF��CDƽ�֡�BCD����֤��EFƽ�֡�BED���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
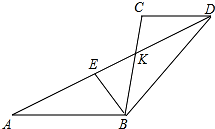 ��ͼ����֪�߶�AB��CD��AD��BC�ཻ�ڵ�K��E���߶�AD��һ���㣮
��ͼ����֪�߶�AB��CD��AD��BC�ཻ�ڵ�K��E���߶�AD��һ���㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ���� | B�� | ����Ϊԭ����5�� | ||
| C�� | ����Ϊԭ����10�� | D�� | ��СΪԭ����$\frac{1}{10}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com