
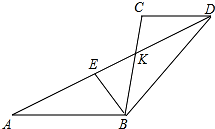
 如图,已知线段AB∥CD,AD与BC相交于点K,E是线段AD上一动点.
如图,已知线段AB∥CD,AD与BC相交于点K,E是线段AD上一动点.分析 (1)由已知得BK=KC,由CD∥AB可证△KCD∽△KBA,利用$\frac{CD}{AB}$=$\frac{CK}{BK}$求值;
(2)AB=BC+CD.作△ABD的中位线,由中位线定理得EF∥AB∥CD,可知G为BC的中点,由平行线及角平分线性质,得∠GEB=∠EBA=∠GBE,则EG=BG=$\frac{1}{2}$BC,而GF=$\frac{1}{2}$CD,EF=$\frac{1}{2}$AB,利用EF=EG+GF求线段AB、BC、CD三者之间的数量关系;
(3)当AE=$\frac{1}{n}$AD(n>2)时,EG=BG=$\frac{1}{n}$BC,而GF=$\frac{1}{n}$CD,EF=$\frac{n-1}{n}$AB,EF=EG+GF可得BC+CD=(n-1)AB.
解答  解:(1)∵BK=KC,
解:(1)∵BK=KC,
∴$\frac{CK}{BK}$=1,
又∵CD∥AB,
∴△KCD∽△KBA,
∴$\frac{CD}{AB}=\frac{CK}{BK}$=1;
(2)当BE平分∠ABC,AE=$\frac{1}{2}$AD时,AB=BC+CD;
证明:取BD的中点为F,连接EF交BC于G点,
由中位线定理,得EF∥AB∥CD,
∴G为BC的中点,∠GEB=∠EBA,
又∵∠EBA=∠GBE,
∴∠GEB=∠GBE,
∴EG=BG=$\frac{1}{2}$BC,而GF=$\frac{1}{2}$CD,EF=$\frac{1}{2}$AB,
∵EF=EG+GF,
即:$\frac{1}{2}$AB=$\frac{1}{2}$BC+$\frac{1}{2}$CD;
∴AB=BC+CD;
(3)由(2)同理可得:当AE=$\frac{1}{n}$AD(n>2)时,EF∥AB,
同理可得:$\frac{BG}{BC}$=$\frac{AE}{AD}$=$\frac{1}{n}$,则BG=$\frac{1}{n}$•BC,则EG=BG=$\frac{1}{n}$•BC,
$\frac{GF}{CD}$=$\frac{BG}{BC}$=$\frac{1}{n}$,则GF=$\frac{1}{n}$•CD,$\frac{EF}{AB}$=$\frac{ED}{AD}$=$\frac{n-1}{n}$,
∴$\frac{1}{n}$+$\frac{1}{n}$•CD=$\frac{n-1}{n}$•AB,
∴BC+CD=(n-1)AB,
故当AE=$\frac{1}{n}$AD(n>2)时,BC+CD=(n-1)AB.
点评 本题考查了平行线的性质,三角形中位线定理,相似三角形的判定与性质,角平分线的性质,正确的作出辅助线构造平行线利用三角形的中位线定理解决问题是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,在矩形ABCD中,AB=12cm,BC=6cm,点P沿AB边从点A开始向点B以2cm/s的速度移动;点Q沿DA边从点D向点A以1cm/s的速度移动.如果P、Q同时出发,用t(s)表示移动时间(0≤t≤6).那么:
如图所示,在矩形ABCD中,AB=12cm,BC=6cm,点P沿AB边从点A开始向点B以2cm/s的速度移动;点Q沿DA边从点D向点A以1cm/s的速度移动.如果P、Q同时出发,用t(s)表示移动时间(0≤t≤6).那么:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com