
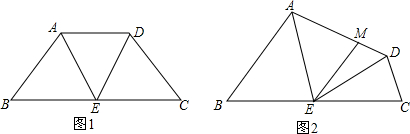
分析 (1)由已知条件易证四边形ABCD是等腰梯形,所以AB=CD,再由已知条件即可证明△ABE≌△DCE,由全等三角形的性质可得AE=DE,又∠AED=60°,所以可证明△ADE是等边三角形;
(2)过点E作EN⊥AB于点N,利用已知得出∠BAE=∠DEC,进而得出△ABE∽△ECD,利用相似三角形的性质求得出∠BAE=∠DAE,得出EN=EM,进而利用特殊角的三角函数值求出即可.
解答 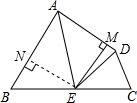 (1)证明:∵AD∥BC,∠B=∠C=60°,
(1)证明:∵AD∥BC,∠B=∠C=60°,
∴AB=CD,
∵E是BC的中点,
∴BE=CE,
在△ABE和△DCE中,
$\left\{\begin{array}{l}{AB=DC}\\{∠B=∠C}\\{BE=CE}\end{array}\right.$,
∴△ABE≌△DCE,
∴AE=DE,
又∵∠AED=60°,
∴△ADE是等边三角形;
(2)解:过点E作EN⊥AB于点N,
∵∠AED=60°,
∴∠AEB+∠DEC=120°,
∵∠B=60°,
∴∠BAE+∠AEB=120°,
∴∠BAE=∠DEC,
又∵∠B=∠C=60°,
∴△ABE∽△ECD,
∴$\frac{AB}{EC}=\frac{AE}{DE}$,
∴AB•ED=EC•EA,
∵E是BC的中点,
∴EB=EC,
∴AB•DE=BE•AE,
∴$\frac{AB}{BE}=\frac{AE}{DE}$,
又∵∠AED=∠B=60°,
∴△ABE∽AED,
∴∠BAE=∠DAE,
∵NE⊥AB,EM⊥AD,
∴NE=EM,
∴sin60°=$\frac{NE}{BE}$$\frac{\sqrt{3}}{2}$,
∵BE=EC,
∴$\frac{EN}{BC}$=$\frac{EM}{BC}$=$\frac{\sqrt{3}}{4}$,
∵BC=4,
∴EM=$\sqrt{3}$.
点评 此题考查了全等三角形的判定和性质以及相似三角形的判定与性质以及角平分线的性质和特殊角的三角函数数值等知识,综合性较强,得出NE=EM是解题关键.


科目:初中数学 来源: 题型:解答题
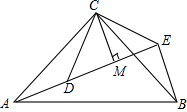 如图,△ACB和△DCE均为等腰三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE.
如图,△ACB和△DCE均为等腰三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 逐渐增大 | B. | 始终等于16 | C. | 始终等于4 | D. | 不能确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
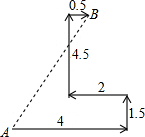 中国机器人创意大赛于2014年7月15日在哈尔滨开幕.如图是一参赛队员设计的机器人比赛时行走的路径,机器人从A处先往东走4m,又往北走1.5m,遇到障碍后又往西走2m,再转向北走4.5m处往东一拐,仅走0.5m就到达了B.问机器人从点A到点B之间的距离是多少?
中国机器人创意大赛于2014年7月15日在哈尔滨开幕.如图是一参赛队员设计的机器人比赛时行走的路径,机器人从A处先往东走4m,又往北走1.5m,遇到障碍后又往西走2m,再转向北走4.5m处往东一拐,仅走0.5m就到达了B.问机器人从点A到点B之间的距离是多少?查看答案和解析>>
科目:初中数学 来源: 题型:填空题
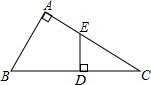 如图,在Rt△ABC中,∠A=90°,∠C=30°,D为斜边上的一点且BD=AB,过点D作BC的垂线,交AC于点E.若△CDE的面积为a,则四边形ABDE的面积为2a.
如图,在Rt△ABC中,∠A=90°,∠C=30°,D为斜边上的一点且BD=AB,过点D作BC的垂线,交AC于点E.若△CDE的面积为a,则四边形ABDE的面积为2a.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com