
【题目】已知:如图,AC∥DF,直线AF分别直线BD、CE 相交于点G、H,∠1=∠2,
求证:∠C=∠D.
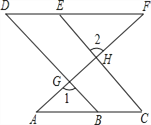
证明: ∵∠1=∠2(已知)
∠1=∠DGH( ),
∴∠2=__________( 等量代换 )
∴__________∥__________( 同位角相等,两直线平行 )
∴∠C=___________( 两直线平行,同位角相等 )
又∵AC∥DF__________
∴∠D=∠ABG_________
∴∠C=∠D__________
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,一次函数y=﹣x+b与反比例函数y= ![]() (k≠0)的图象相交于A(﹣1,4)、B(4,﹣1)两点,直线l⊥x轴于点E(﹣4,0),与反比例函数和一次函数的图象分别相交于点C、D,连接AC、BC
(k≠0)的图象相交于A(﹣1,4)、B(4,﹣1)两点,直线l⊥x轴于点E(﹣4,0),与反比例函数和一次函数的图象分别相交于点C、D,连接AC、BC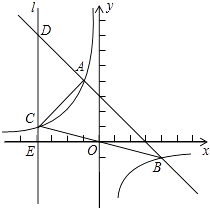
(1)求出b和k;
(2)求证:△ACD是等腰直角三角形;
(3)在y轴上是否存在点P,使S△PBC=S△ABC?若存在,请求出P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了响应市委和市政府“绿色环保,节能减排”的号召,幸福商场用3300元购进甲、乙两种节能灯共计100只,很快售完.这两种节能灯的进价、售价如下表:
进价(元/只) | 售价(元/只) | |
甲种节能灯 | 30 | 40 |
甲种节能灯 | 35 | 50 |
(1)求幸福商场甲、乙两种节能灯各购进了多少只?
(2)全部售完100只节能灯后,商场共计获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周末,小明坐公交车到滨海公园游玩,他从家出发0.8小时后达到中心书城,逗留一段时间后继续坐公交车到滨海公园,小明离家一段时间后,爸爸驾车沿相同的路线前往海滨公园. 如图是他们离家路程s(km)与小明离家时间t(h)的关系图,请根据图回答下列问题:
(1)图中自变量是____,因变量是______;
(2)小明家到滨海公园的路程为____ km,小明在中心书城逗留的时间为____ h;
(3)小明出发______小时后爸爸驾车出发;
(4)图中A点表示___________________________________;
(5)小明从中心书城到滨海公园的平均速度为______km/h,小明爸爸驾车的平均速度为______km/h;(补充;爸爸驾车经过______追上小明);
(6)小明从家到中心书城时,他离家路程s与坐车时间t之间的关系式为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形![]() 的各边分别平行于
的各边分别平行于![]() 轴或
轴或![]() 轴,物体甲和物体乙分别由点
轴,物体甲和物体乙分别由点![]() 同时出发,沿长方形
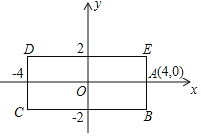
同时出发,沿长方形![]() 的边作环绕运动.物体甲按逆时针方向以2个单位/秒匀速运动,物体乙按顺时针方向以4个单位/秒匀速运动,则两个物体运动后的第2020次相遇地点的坐标是____.
的边作环绕运动.物体甲按逆时针方向以2个单位/秒匀速运动,物体乙按顺时针方向以4个单位/秒匀速运动,则两个物体运动后的第2020次相遇地点的坐标是____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法错误的是( )
A. 任意抛掷一个啤酒瓶盖,落地后印有商标一面向上的可能性大小是![]()
B. 一个转盘被分成8块全等的扇形区域,其中2块是红色,6块是蓝色. 用力转动转盘,当转盘停止后,指针对准红色区域的可能性大小是![]()
C. 一个不透明的盒子中装有2个白球,3个红球,这些球除颜色外都相同. 从这个盒子中随意摸出一个球,摸到白球的可能性大小是![]()
D. 100件同种产品中,有3件次品. 质检员从中随机取出一件进行检测,他取出次品的可能性大小是![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°,∠ABC=30°,AC=2,△ABC绕点C顺时针旋转得△A1B1C,当A1落在AB边上时,连接B1B,取BB1的中点D,连接A1D,则A1D的长度是( ) 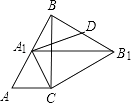
A.![]()
B.2 ![]()
C.3
D.2 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=5,BC=8,D是线段BC上的动点(不含端点B、C).若线段AD长为正整数,则点D的个数共有( )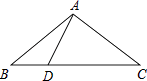
A.5个
B.4个
C.3个
D.2个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com