
分析 ①△ABC是锐角三角形时,先根据高线的定义求出∠ADB=90°,∠BEC=90°,然后根据直角三角形两锐角互余求出∠ABD,再根据三角形的一个外角等于与它不相邻的两个内角的和列式进行计算即可得解;
②△ABC是钝角三角形时,根据直角三角形两锐角互余求出∠BHC=∠A,从而得解.
解答 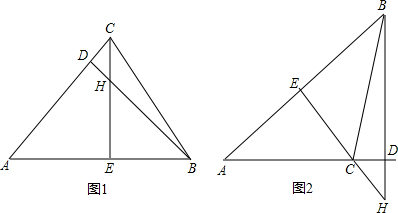 解:①如图1,△ABC是锐角三角形时,
解:①如图1,△ABC是锐角三角形时,
∵BD、CE是△ABC的高线,
∴∠ADB=90°,∠BEC=90°,
在△ABD中,∵∠A=40°,
∴∠ABD=90°-40°=50°,
∴∠BHC=∠ABD+∠BEC=50°+90°=140°;
②如图2,△ABC是钝角三角形时,
∵BD、CE是△ABC的高线,
∴∠A+∠ACE=90°,∠BHC+∠HCD=90°,
∵∠ACE=∠HCD(对顶角相等),
∴∠BHC=∠A=40°.
综上所述,∠BHC的度数是140°或40°.
故答案为:140°或40°
点评 本题主要考查了三角形的内角和定理,三角形的高线,难点在于要分△ABC是锐角三角形与钝角三角形两种情况讨论,作出图形更形象直观.


 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2,6 | B. | 12,16 | C. | 16,20 | D. | 20,24 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
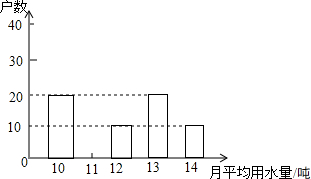 市政府决定对市直机关500户家庭的用水情况作一次调查,调查小组随机抽查了其中的100户家庭一年的月平均用水量(单位:吨),并将调查结果制成了如图所示的条形统计图.
市政府决定对市直机关500户家庭的用水情况作一次调查,调查小组随机抽查了其中的100户家庭一年的月平均用水量(单位:吨),并将调查结果制成了如图所示的条形统计图.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com