
 已知直线y=kx+b与x轴、y轴分别交于A、B两点,与反比例函数y=$\frac{a}{x}$交于一象限内的P($\frac{1}{2}$,n),Q(4,m)两点,且tan∠BOP=$\frac{1}{8}$.
已知直线y=kx+b与x轴、y轴分别交于A、B两点,与反比例函数y=$\frac{a}{x}$交于一象限内的P($\frac{1}{2}$,n),Q(4,m)两点,且tan∠BOP=$\frac{1}{8}$.分析 (1)过P作PC⊥y轴于C,由P($\frac{1}{2}$,n),得到OC=n,PC=$\frac{1}{2}$,根据三角函数的定义得到P($\frac{1}{2}$,4),于是得到反比例函数的解析式为y=$\frac{2}{x}$,Q(4,$\frac{1}{2}$),解方程组即可得到直线的函数表达式为y=-x+$\frac{9}{2}$;
(2)过Q作OD⊥y轴于D,于是得到S△POQ=S四边形PCDQ=$\frac{63}{8}$;
(3)观察图象可得结果.
解答 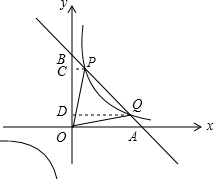 解:(1)过P作PC⊥y轴于C,
解:(1)过P作PC⊥y轴于C,
∵P($\frac{1}{2}$,n),
∴OC=n,PC=$\frac{1}{2}$,
∵tan∠BOP=$\frac{1}{8}$,
∴n=4,
∴P($\frac{1}{2}$,4),
设反比例函数的解析式为y=$\frac{a}{x}$,
∴a=4,
∴反比例函数的解析式为y=$\frac{2}{x}$,
∴Q(4,$\frac{1}{2}$),
把P($\frac{1}{2}$,4),Q(4,$\frac{1}{2}$)代入y=kx+b中得,
$\left\{\begin{array}{l}{4=\frac{1}{2}k+b}\\{\frac{1}{2}=4k+b}\end{array}\right.$,
∴$\left\{\begin{array}{l}{k=-1}\\{b=\frac{9}{2}}\end{array}\right.$,
∴直线的函数表达式为y=-x+$\frac{9}{2}$;
(2)过Q作QD⊥y轴于D,
则S△POQ=S四边形PCDQ=$\frac{1}{2}$×($\frac{1}{2}$+4)×(4-$\frac{1}{2}$)=$\frac{63}{8}$;
(3)由图象知,
当-x+$\frac{9}{2}$>$\frac{2}{x}$时,$\frac{1}{2}<x<4$或x<0
点评 本题考查了反比例函数与一次函数的交点问题,反比例函数图象上点的坐标特征,利用待定系数法求反比例函数和一次函数的解析式,正切函数的定义,难度适中,利用数形结合是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在⊙O中,AB是直径,CO⊥AB,D是CO的中点,DE∥AB,求证:$\widehat{EC}$=2$\widehat{BE}$.
如图,在⊙O中,AB是直径,CO⊥AB,D是CO的中点,DE∥AB,求证:$\widehat{EC}$=2$\widehat{BE}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图:某通信公司在A区 要修建一座信号发射塔M,要求发射塔到两城镇P、Q的距离相等,同时到两条高速公路l1、l2的距离也相等.请用直尺和圆规在图中作出发射塔M的位置.(不写作法,保留作图痕迹 )
如图:某通信公司在A区 要修建一座信号发射塔M,要求发射塔到两城镇P、Q的距离相等,同时到两条高速公路l1、l2的距离也相等.请用直尺和圆规在图中作出发射塔M的位置.(不写作法,保留作图痕迹 )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com