
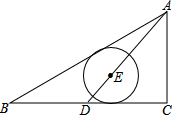
 如图,Rt△ABC中,∠C=90°,AB=5,AC=3,D点从BC的中点到C点运动,点E在AD上,以E为圆心的⊙E分别与AB、BC相切,则⊙E的半径R的取值范围为( )
如图,Rt△ABC中,∠C=90°,AB=5,AC=3,D点从BC的中点到C点运动,点E在AD上,以E为圆心的⊙E分别与AB、BC相切,则⊙E的半径R的取值范围为( )A、
| ||||
B、
| ||||
C、
| ||||
D、1≤R≤
|
| 13 |
| ||
| 3 |
| 2 |
| 3 |
| 13 |
| ||
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 13 |
| ||
| 3 |
| 6 |
| 7 |
| 4 |
| 3 |
| 6 |
| 7 |
| 4 |
| 3 |
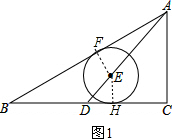
| AB2-AC2 |
| AC2+CD2 |
| 13 |
| DE |
| DA |
| EH |
| AC |
| DH |
| DC |
| DE | ||
|
| R |
| 3 |
| DH |
| 2 |
| ||
| 3 |
| 2 |
| 3 |
| 13 |
| ||
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 13 |
| ||
| 3 |
| 6 |
| 7 |
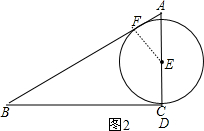 当点D运动到点C的位置,如图2,作EF⊥AB于F,
当点D运动到点C的位置,如图2,作EF⊥AB于F,| EF |
| BC |
| AE |
| AB |
| R |
| 4 |
| 3-R |
| 5 |
| 4 |
| 3 |
| 6 |
| 7 |
| 4 |
| 3 |


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
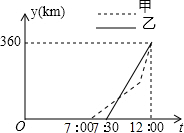 甲、乙两车从A地前往B地,甲车行至AB的中点C处后,以原来速度的1.5倍继续行驶,在整个行程中,汽车离开A地的距离y与时刻t的对应关系如图所示,求:
甲、乙两车从A地前往B地,甲车行至AB的中点C处后,以原来速度的1.5倍继续行驶,在整个行程中,汽车离开A地的距离y与时刻t的对应关系如图所示,求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com