
【题目】某电器商城销售A、B两种型号的电风扇,进价分别为160元、120元,下表是近两周的销售情况:
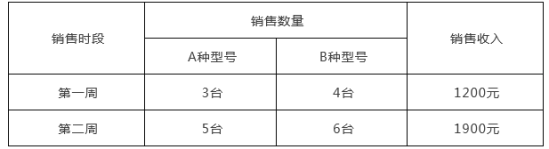
(1)求A、B两种型号的电风扇的销售单价;
(2)若商城准备用不多于7500元的金额再采购这两种型号的电风扇共50台,求A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,商城要求至少购买A型电风扇35台,商场共有几种进货方案?并给出利润最大的方案?
【答案】(1)A、B两种型号电风扇的销售单价分别为200元、150元;(2)37台;(3)三种进货方案,利润最大的方案为采购A种型号的电风扇37台,B种型号的电风扇13台.
【解析】
(1)设A、B两种型号电风扇的销售单价分别为x元、y元,根据3台A型号4台B型号的电扇收入1200元,5台A型号6台B型号的电扇收入1900元,列方程组求解;
(2)设采购A种型号电风扇a台,则采购B种型号电风扇(50a)台,根据金额不多于7500元,列不等式求解;
(3)根据(2)中条件可得出有三种方案,根据A种型号电风扇的进价和售价、B种型号电风扇的进价和售价列出总利润函数关系式,再根据函数关系式性质,代入a的值,即可得出答案.
解:(1)设A、B两种型号电风扇的销售单价分别为x元、y元,
依题意得:
![]() ,解得
,解得![]() ,
,
答:A、B两种型号电风扇的销售单价分别为200元、150元.
(2)设采购A种型号电风扇a台,则采购B种型号电风扇(50a)台.
依题意得:160a+120(50a)≤7500,
解得:a≤![]() .
.
答:超市最多采购A种型号电风扇37台时,采购金额不多于7500元.
(3)在(2)的条件下,可行方案有三种:
当a=35时,采购A种型号的电风扇35台,B种型号的电风扇15台;
当a=36时,采购A种型号的电风扇36台,B种型号的电风扇14台;
当a=37时,采购A种型号的电风扇37台,B种型号的电风扇13台.
根据题意得:利润的函数关系式为:
y=(200160)a+(150120)(50a)
即y=10a+1500,
当a越大时,y越大,
∴当a=37时,最大利润y=1870(元)
∴最大利润的方案为采购A种型号的电风扇37台,B种型号的电风扇13台.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,一种某小区的两幢10层住宅楼间的距离为AC=30m,由地面向上依次为第1层、第2层、…、第10层,每层高度为3m.假设某一时刻甲楼在乙楼侧面的影长EC=h,太阳光线与水平线的夹角为α
(1)用含α的式子表示h(不必指出α的取值范围);
(2)用含α的式子表示h(不必指出α的取值范围);
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线 AB与 x 轴,y 轴分别交于点 A和点 B,点 A的坐标为(1,0),且 2OA=OB.
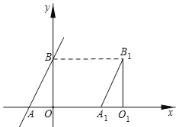
(1)求直线 AB 解析式;
(2)如图,将△A O B 向右平移 3 个单位长度,得到△A1O1B1,求线段 O B1的长;
(3)在(2)中△AOB 扫过的面积是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,四边形OABC为矩形,OA在x轴正半轴上,OC在y轴正半轴上,且A(10,0)、C(0,8)
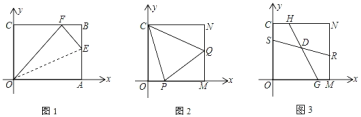
(1)如图1,在矩形OABC的边AB上取一点E,连接OE,将△AOE沿OE折叠,使点A恰好落在BC边上的F处,求AE的长;
(2)将矩形OABC的AB边沿x轴负方向平移至MN(其它边保持不变),M、N分别在边OA、CB上且满足CN=OM=OC=MN.如图2,P、Q分别为OM、MN上一点.若∠PCQ=45°,求证:PQ=OP+NQ;
(3)如图3,S、G、R、H分别为OC、OM、MN、NC上一点,SR、HG交于点D.若∠SDG=135°,HG=4![]() ,求RS的长.
,求RS的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=40°,△ABC的外角∠CBD的平分线BE交AC的延长线于点E.
(1)求∠CBE的度数;
(2)过点D作DF∥BE,交AC的延长线于点F,求∠F的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
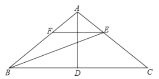
【题目】如图,在△ABC中,AB=AC,D是BC边上的中点,连接AD,BE平分∠ABC交AC于点E,过E作EF∥BC交AB于点F.
(1)若∠C=36°,求∠BAD的度数;
(2)求证:FB=FE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的顶点都在正方形网格的格点(网格线的交点)上.
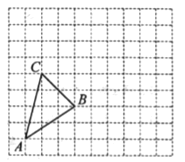
(1)画出△ABC先向右平移5个单位长度,再向上平移2个单位长度所得的△A1B1C1;
(2)画出△ABC的中线AD;
(3)画出△ABC的高CE所在直线,标出垂足E:
(4)在(1)的条件下,线段AA1和CC1的关系是
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=3,BC=9,把矩形ABCD沿对角线BD折叠,使点C与点F重合,BF交AD于点M,过点C作CE⊥BF于点E,交AD于点G,则MG的长= . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com