
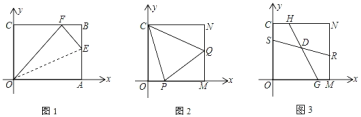
【题目】在平面直角坐标系xOy中,四边形OABC为矩形,OA在x轴正半轴上,OC在y轴正半轴上,且A(10,0)、C(0,8)
(1)如图1,在矩形OABC的边AB上取一点E,连接OE,将△AOE沿OE折叠,使点A恰好落在BC边上的F处,求AE的长;
(2)将矩形OABC的AB边沿x轴负方向平移至MN(其它边保持不变),M、N分别在边OA、CB上且满足CN=OM=OC=MN.如图2,P、Q分别为OM、MN上一点.若∠PCQ=45°,求证:PQ=OP+NQ;
(3)如图3,S、G、R、H分别为OC、OM、MN、NC上一点,SR、HG交于点D.若∠SDG=135°,HG=4![]() ,求RS的长.
,求RS的长.
【答案】(1)AE=5;(2)见解析;(3)![]() .
.
【解析】
(1)设![]() ,在
,在![]() 中,根据勾股定理列方程解出即可;
中,根据勾股定理列方程解出即可;
(2)作辅助线,构建两个三角形全等,证明![]() 和
和![]() ,由
,由![]() ,得出结论;
,得出结论;
(3)作辅助线,构建平行四边形和全等三角形,可得![]() 和
和![]() ,则
,则![]() ,
,![]() ,证明
,证明![]() 和
和![]() ,得
,得![]() ,设
,设![]() ,在
,在![]() 中,根据勾股定理列方程求出EN的长,再利用勾股定理求CE,则SR与CE相等,即可得出结论.
中,根据勾股定理列方程求出EN的长,再利用勾股定理求CE,则SR与CE相等,即可得出结论.
(1)如图1,由题意得:![]() ,
,![]() ,
,
设![]() ,则
,则![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
由勾股定理得:![]() ,
,
解得:![]() ,
,
∴![]() ;
;
(2)如图2,在PO的延长线上取一点E',使![]() ,
,
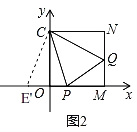
∵![]() ,
,![]() ,
,
∴四边形OMNC是正方形,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ;
;
②如图3,过C作![]() ,在x轴负半轴上取一点E′,使
,在x轴负半轴上取一点E′,使![]() ,得
,得![]() ,
,
且![]() ,则
,则![]() ,
,

过C作![]() 交OM于F,连接FE,得
交OM于F,连接FE,得![]() ,则
,则![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]()
在![]() 中,
中,![]() ,
,![]() ,
,
根据勾股定理得:![]() ,
,
∴![]() ,
,
设![]() ,则
,则![]() ,
,![]() ,
,
则![]() ,
,
解得:![]() ,
,
∴![]() ,
,
根据勾股定理得:![]() ,
,
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】已知△ABC中,BE平分∠ABC,点P在射线BE上.

(1)如图1,若∠ABC=40°,CP∥AB,求∠BPC的度数;
(2)如图2,若∠BAC=100°,∠PBC=∠PCA,求∠BPC的度数;
(3)若∠ABC=40°,∠ACB=30°,直线CP与△ABC的一条边垂直,画出相应图形并求∠BPC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料,根据材料回答:
例如1:(-2)3×33=(-2)×(-2)×(-2)×3×3×3
=[(-2)×3]×[(-2)×3]×[(-2)×3]
=[(-2)×3]3=(-6)3=-216.
例如2:
86×0.1256=8×8×8×8×8×8×0.125×0.125×0.125×0.125×0.125×0.125
=(8×0.125)×(8×0.125)×(8×0.125)×(8×0.125)×(8×0.125)×(8×0.125)
=(8×0.125)6=1.
(1)仿照上面材料的计算方法计算: ;
;
(2)由上面的计算可总结出一个规律:(用字母表示)an·bn=_______________;
(3)用(2)的规律计算:-0.42018× ×
×![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为 2 的正方形 ABCD 中剪去一个边长为 1 的小正方形 EFGD ,动点 P 从点 A 出发,沿A E F G C B 的路线,绕多边形的边匀速运动到点 B 时停止,则 ABP 的面积 S 随着时间t 变化的函数图象大致是( )

A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为了测量某建筑物BC的高度,小明先在地面上用测角仪自A处测得建筑物顶部的仰角是30°,然后在水平地而上向建筑物前进了50m到达D处,此时遇到一斜坡,坡度i=1: ![]() ,沿着斜坡前进20米到达E处测得建筑物顶部的仰角是45°,(坡度i=1:
,沿着斜坡前进20米到达E处测得建筑物顶部的仰角是45°,(坡度i=1: ![]() 是指坡面的铅直高度FE与水平宽度DE的比).请你计算出该建筑物BC的高度.(取
是指坡面的铅直高度FE与水平宽度DE的比).请你计算出该建筑物BC的高度.(取 ![]() =1.732,结果精确到0.1m).
=1.732,结果精确到0.1m).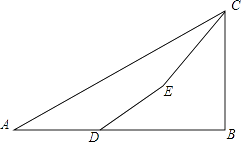
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电器商城销售A、B两种型号的电风扇,进价分别为160元、120元,下表是近两周的销售情况:
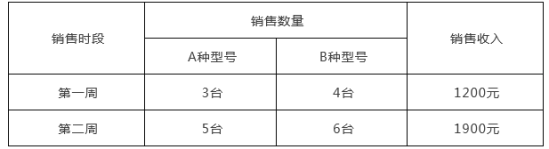
(1)求A、B两种型号的电风扇的销售单价;
(2)若商城准备用不多于7500元的金额再采购这两种型号的电风扇共50台,求A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,商城要求至少购买A型电风扇35台,商场共有几种进货方案?并给出利润最大的方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
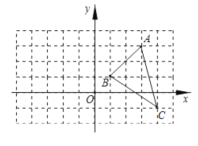
【题目】如图,△ABC的三个顶点坐标分别是A(3,3),B(1,1),C(4,-1).
(1)直接写出点A,B,C关于x轴对称的点A1,B1,C1,的坐标:A1( , ),B1( , ),C1( , ).
(2)在图中作出△ABC关于y轴对称的图象△A2B2C2.
(3)在y轴上求作一点P,使得PA+PB的值最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平面直角坐标系xOy中,直线AB与x轴交于点A(﹣2,0),与反比例函数在第一象限内的图象的交于点B(2,n),连接BO,若S△AOB=4.
(1)求该反比例函数的解析式和直线AB的解析式;
(2)若直线AB与双曲线的另一交点为D点,求△ODB的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com