
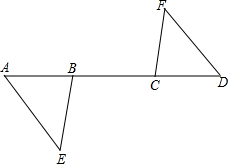
 已知:如图,A,B,C,D四点在一条直线上,AC=BD,AE∥DF,∠ABE=∠DCF,求证:△ABE≌△DCF.
已知:如图,A,B,C,D四点在一条直线上,AC=BD,AE∥DF,∠ABE=∠DCF,求证:△ABE≌△DCF. 分析 首先利用平行线的性质得出∠A=∠D,再由AC=BD得出AB=CD,进而利用全等三角形的判定定理ASA即可证明△ABE≌△DCF.
解答 证明:∵AE∥DF,
∴∠A=∠D,
∵AC=BD,
∴AB=CD,
在△ABE和△DCF中,
$\left\{\begin{array}{l}{∠A=∠D}\\{AB=DC}\\{∠ABE=∠DCF}\end{array}\right.$,
∴△ABE≌△DCF(ASA).
点评 本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.


科目:初中数学 来源: 题型:填空题
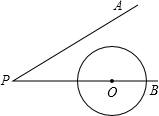 如图,∠APB=30°⊙O半径为1cm,圆心O在PB上,OP=3cm,若⊙O沿BP方向移动,当⊙O与直线PA相切时,圆心O移动的距离为1或5cm.
如图,∠APB=30°⊙O半径为1cm,圆心O在PB上,OP=3cm,若⊙O沿BP方向移动,当⊙O与直线PA相切时,圆心O移动的距离为1或5cm.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-3,-2) | B. | (-2,-3) | C. | (2,3) | D. | (3,2) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
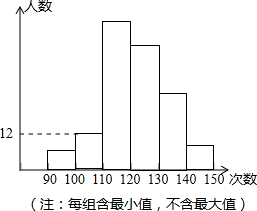 某校为了了解九年级学生的体能情况,抽调了一部分学生进行一分钟跳绳测试,将测试成绩整理后作出如下统计图.甲同学计算出前两组的频率和是0.12,乙同学计算出跳绳次数不少于100次的同学占96%,丙同学计算出从左至右第二、三、四组的频数比为4:17:15.结合统计图回答下列问题:
某校为了了解九年级学生的体能情况,抽调了一部分学生进行一分钟跳绳测试,将测试成绩整理后作出如下统计图.甲同学计算出前两组的频率和是0.12,乙同学计算出跳绳次数不少于100次的同学占96%,丙同学计算出从左至右第二、三、四组的频数比为4:17:15.结合统计图回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
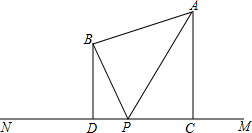 加油站A和商店B在马路MN的同一侧,A到MN的距离为5米,B到MN的距离为3米,DC=6米,行人P在马路MN上行走.P到A的距离与P到B的距离之和最小等于几米?
加油站A和商店B在马路MN的同一侧,A到MN的距离为5米,B到MN的距离为3米,DC=6米,行人P在马路MN上行走.P到A的距离与P到B的距离之和最小等于几米?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
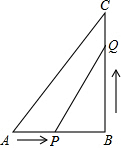 如图所示,△ABC中,AB=6cm,BC=8cm,∠B=90°,点P从点A开始沿AB边向B以1cm/s的速度移动,点Q从B点开始沿BC边向点C以2cm/s的速度移动.如果p、Q分别从A、B同时出发,移动了t秒:
如图所示,△ABC中,AB=6cm,BC=8cm,∠B=90°,点P从点A开始沿AB边向B以1cm/s的速度移动,点Q从B点开始沿BC边向点C以2cm/s的速度移动.如果p、Q分别从A、B同时出发,移动了t秒:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com