
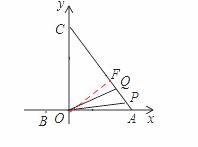
如图,已知二次函数 的图象经过点A、
的图象经过点A、 B和点C.连接AC,有两动点P、Q同时从点O出发,其中点P以每秒3个单位长度的速度沿折线OAC按O→A→C的路线运动,点Q以每秒8个单位长度的速度沿折线OCA按O→C→A的路线运动,当P、Q两点相遇时,它们都停止运动,设P、Q同时从点O出发t秒时,△OPQ的面
B和点C.连接AC,有两动点P、Q同时从点O出发,其中点P以每秒3个单位长度的速度沿折线OAC按O→A→C的路线运动,点Q以每秒8个单位长度的速度沿折线OCA按O→C→A的路线运动,当P、Q两点相遇时,它们都停止运动,设P、Q同时从点O出发t秒时,△OPQ的面 积为S.
积为S.
(1)请求出S关于t的函数关系式, 并写出自变量t的取值范围;
并写出自变量t的取值范围;
(2)设S0是②中函数S的 最大值,求出S0的值.
最大值,求出S0的值.
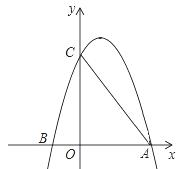
解:(1)∵二次函数的图象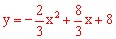 经过点A、B和点C,
经过点A、B和点C,
∴令y=0,得x=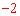 或x=6;令x=0,得y=8。
或x=6;令x=0,得y=8。
∴A(6,0),C(0,8)。
分三种情况讨论如下,

情况1:当0≤t≤1时,如图1,
S=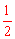 OP•OQ=
OP•OQ=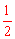 ×3t×8t=12t2。
×3t×8t=12t2。
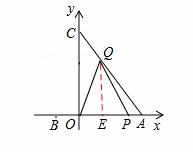
情况2:当1<t≤2时,如图2,
作QE⊥OA,垂足为E,
S=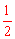 OP•EQ=
OP•EQ=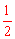 ×3t×
×3t×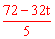
 。
。

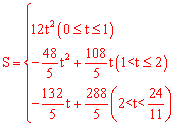 。
。
(2)根据(1)的函数即可得出S的最大值:
当0≤t≤1时,S =12t2,函数的最大值是12;
=12t2,函数的最大值是12;
当1<t≤2时,S ,函数的最大值是
,函数的最大值是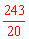 ;
;
当2<t<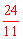
 ,S=
,S=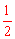 QP•OF
QP•OF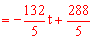 ,函数的最大值不超过
,函数的最大值不超过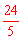
 。
。
∴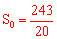 。
。
【考点】二次函数综合题,单双动点问题,曲线上点的坐标与方程 的关
的关 系,由实际问题列函数关系
系,由实际问题列函数关系 式,一次函数和二次函数的性质,分类思想、数形结合思想的应用。
式,一次函数和二次函数的性质,分类思想、数形结合思想的应用。



科目:初中数学 来源: 题型:
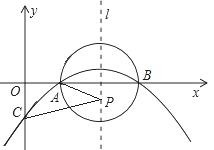
如图,已知抛物线y=ax2+bx+c(a≠0)的顶点坐标为(4,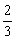 ),且与y轴交于点C(0,
),且与y轴交于点C(0,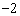 ),与x轴交于A,B两点(点A在点B的左边)。
),与x轴交于A,B两点(点A在点B的左边)。
(1)求抛物线的解析式及A,B两点的坐标;
(2)在(1)中抛物线的对称轴l上是否存在一点P,使AP+CP的值最小?若存在,求AP+CP的最小值,若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
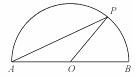
如图 ,点P是以O为圆心,AB为直径的半圆上的动点,AB=2,设弦AP的长为x,△APO的面积为y,则当y=
,点P是以O为圆心,AB为直径的半圆上的动点,AB=2,设弦AP的长为x,△APO的面积为y,则当y= 时,x的取
时,x的取 值是【 】
值是【 】
A. 1 B. 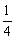 C. 1或
C. 1或 D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
阅读下列材料:
小华遇到这样一个问题,如图1,△ABC中,∠ACB=30º,BC=6,AC=5,在△ABC内部有一点P,连接PA.PB.PC,求PA+PB+PC的最小值.

小华是这样思考的:要解决这个问题,首先应想办法将这三条端点重合于一点的线段分离,然后再将它们连接成一条折线,并让折线的两个端点为定点,这样依据“两点之间,线段最短”,就可以求出这三条线段和的最小值了.他先后尝试了翻折.旋转.平移的方法,发现通过旋转可以解决这个问题.他的做法是,如图2,将△APC绕点C顺时针旋转60º,得到△EDC,连接PD.BE,则BE的长即为所求.
(1)请你写出图2中,PA+PB+PC的最小值为 ;
(2)参考小华的思考问题的方法,解决下列问题:
①如图3,菱形ABCD中,∠ABC=60º,在菱形ABCD内部有一点P,请在图3中画出并指明长度等于PA+PB+PC最小值的线段(保留画图痕迹,画出一条即可);
②若①中菱形ABCD的边长为4,请直接写出当PA+PB+P C值最小时PB的长.
C值最小时PB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
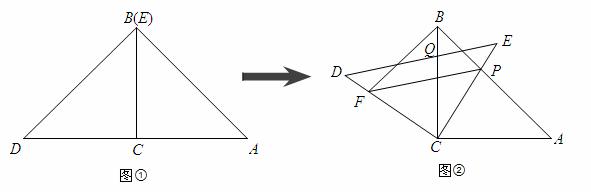
将两块全等的三角板如图①摆放,其中∠ACB=∠DCE=90°,∠A=∠D=45°,将图①中的△DCE顺时针旋转得图② ,点P是AB与CE的交点,点Q是DE
,点P是AB与CE的交点,点Q是DE 与BC的交点,在DC上取
与BC的交点,在DC上取 一点F,连接BE、FP,设BC=1,当BF⊥AB时,求△PBF面积的最大值。
一点F,连接BE、FP,设BC=1,当BF⊥AB时,求△PBF面积的最大值。
查看答案和解析>>
科目:初中数学 来源: 题型:
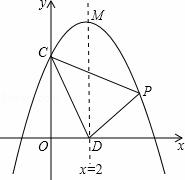
如图,在平面直角坐标系xOy中,抛物线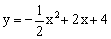 交y轴于点C
交y轴于点C ,对称轴与x轴交于点D,顶点为M,设点P(x,y)是第一象限内该抛物线上的一个动点,直线PE绕点P旋转,
,对称轴与x轴交于点D,顶点为M,设点P(x,y)是第一象限内该抛物线上的一个动点,直线PE绕点P旋转, 与y轴交于点E,是否存在以O、P、E为顶点的三角形与△OPD全等?若存在,请求出点E的坐标;若不存在,请说明理由。
与y轴交于点E,是否存在以O、P、E为顶点的三角形与△OPD全等?若存在,请求出点E的坐标;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知在平面直角坐标系中,四边形ABCO是梯形,且BC∥AO,其中A(6,0),B(3,
 ),∠AOC=60°,动点P从点O以每秒2个单位的速度向点A运动,动点Q也同时从点B沿B→C→O的线路以每秒1个单位的速度向点O运动,当点P到达A点
),∠AOC=60°,动点P从点O以每秒2个单位的速度向点A运动,动点Q也同时从点B沿B→C→O的线路以每秒1个单位的速度向点O运动,当点P到达A点 时,点Q也随之停止,设
时,点Q也随之停止,设 点P,Q运
点P,Q运 动的时间为t(秒).
动的时间为t(秒).
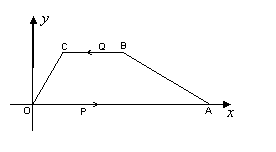

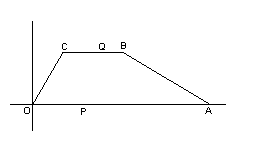

(1)求点C的坐标及梯形ABCO的面积;
 (2)当点Q在CO边上运动时,求△OPQ的面积S与运动时间t的函数关系式,并写出自变量t的取值范围;
(2)当点Q在CO边上运动时,求△OPQ的面积S与运动时间t的函数关系式,并写出自变量t的取值范围;
(3)以O,P,Q为顶点的三角形能构成直角三角形吗?若能,请求出t 的值;若不能,请说明理由.
的值;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图1,将由5个边长为1的小正方形组成的十字形纸板沿虚线剪拼成一个大正方形,需剪4
刀。
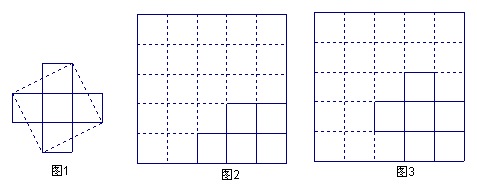

思考发现:大正方形的面积等于5个小正方形的面积和,大正方形的边长等于_______。
实践操作:如图2,将网格中5个边长为1的小正方形组成的图形纸板剪拼成一个大正方形,要求剪
两刀,画出剪拼的痕迹。
智力开发:将网格中的5个边长为1的正方形组成的十字形纸 板,要求只剪2刀也拼成一个大正方形。
板,要求只剪2刀也拼成一个大正方形。
在图中用虚线画出剪拼的痕迹。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com