
【题目】将反比例函数![]() 的图像绕着原点O顺时针旋转45°得到新的双曲线图像
的图像绕着原点O顺时针旋转45°得到新的双曲线图像![]() (如图1所示),直线
(如图1所示),直线![]() 轴,F为x轴上的一个定点,已知,图像
轴,F为x轴上的一个定点,已知,图像![]() 上的任意一点P到F的距离与直线l的距离之比为定值,记为e,即
上的任意一点P到F的距离与直线l的距离之比为定值,记为e,即![]() .
.
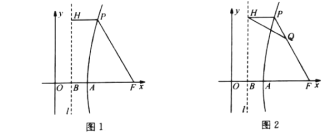
(1)如图1,若直线l经过点B(1,0),双曲线![]() 的解析式为
的解析式为![]() ,且
,且![]() ,则F点的坐标为__________.
,则F点的坐标为__________.
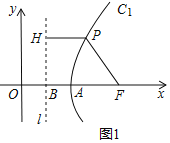
(2)如图2,若直线l经过点B(1,0), 双曲线![]() 的解析式为
的解析式为![]() ,且
,且![]() ,P为双曲线
,P为双曲线![]() 在第一象限内图像上的动点,连接PF,Q为线段PF上靠近点P的三等分点,连接HQ,在点P运动的过程中,当
在第一象限内图像上的动点,连接PF,Q为线段PF上靠近点P的三等分点,连接HQ,在点P运动的过程中,当![]() 时,点P的坐标为__________.
时,点P的坐标为__________.
【答案】F(4,0) ![]()
【解析】
(1)令y=0求出x的值,结合e=2可得出点A的坐标,由点B的坐标及e=2可求出AF的长度,将其代入OF=OB+AB+AF中即可求出点F的坐标;
(2)设点P的坐标为(x,![]() ),则点H的坐标为(1,
),则点H的坐标为(1,![]() ),由Q为线段PF上靠近点P的三等分点,可得出点Q的坐标为(x+
),由Q为线段PF上靠近点P的三等分点,可得出点Q的坐标为(x+![]() ,
,![]() ),利用两点间的距离公式列方程解答即可;
),利用两点间的距离公式列方程解答即可;
解:(1)如图:
当y=0时,±![]() ,
,
解得:x1=2,x2=-2(舍去),
∴点A的坐标为(2,0).
∵点B的坐标为(1,0),
∴AB=1.
∵e=2,
∴![]() ,
,
∴AF=2,
∴OF=OB+AB+AF=4,
∴F点的坐标为(4,0).
故答案为:(4,0).
(2)设点P的坐标为(x,![]() ),则点H的坐标为(1,
),则点H的坐标为(1,![]() ).
).
∵点Q为线段PF上靠近点P的三等分点,点F的坐标为(5,0),
∴点Q的坐标为(x+![]() ,
,![]() ).
).
∵点H的坐标为(1,![]() ),HQ=
),HQ=![]() HP,
HP,
∴(x+![]() -1)2+(
-1)2+(![]() -
-![]() )2=[
)2=[![]() (x-1)]2,
(x-1)]2,
化简得:15x2-48x+39=0,
解得:x1=![]() ,x2=1(舍去),
,x2=1(舍去),
∴点P的坐标为(![]() ,
,![]() ).
).
故答案为:(![]() ,
,![]() ).
).


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某种商品每天的销售利润y(元)与销售单价x(元)之间满足关系y=mx2+20x+n,其图象如图所示.
(1)m=_____,n=_____.
(2)销售单价为多少元时,该种商品每天的销售利润最大?最大利润为多少元?
(3)该种商品每天的销售利润不低于16元时,直接写出x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂设计了一款成本为20元/件的工艺品投放市场进行试销,经过调查,得到如下数据:
销售单价x(元∕件) | … | 30 | 40 | 50 | 60 | … |
每天销售量y(件) | … | 500 | 400 | 300 | 200 | … |
(1)研究发现,每天销售量y与单价x满足一次函数关系,求出y与x的关系式;
(2)当地物价部门规定,该工艺品销售单价最高不能超过45元/件,那么销售单价定为多少时,工艺厂试销该工艺品每天获得的利润8000元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一次军事演习中,蓝方在一条东西走向的公路上的A处朝正南方向撤退,红方在公路上的B处沿南偏西60°方向前进实施拦截,红方行驶1000米到达C处后,因前方无法通行,红方决定调整方向,再朝南偏西45°方向前进了相同的距离,刚好在D处成功拦截蓝方,求拦截点D处到公路的距离(结果不取近似值).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小刚准备用一段长50米的篱笆围成一个三角形形状的场地,用于饲养鸡,已知第一条边长为m米,由于条件限制第二条边长只能比第一条边长的3倍少2米.
(1)用含m的式子表示第三条边长;
(2)第一条边长能否为10米?为什么?
(3)若第一条边长最短,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
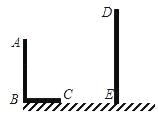
【题目】如图,AB和DE是直立在地面上的两根立柱.AB=5m,某一时刻AB在阳光下的投影BC=3m,同时测量出DE在阳光下的投影长为6m.
(1)请你在图中画出此时DE在阳光下的投影;
(2)请你计算DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
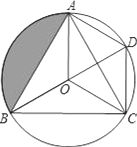
【题目】如图,O是等边△ABC的外心,BO的延长线和⊙O相交于点D,连接DC,DA,OA,OC.
(1)求证:△BOC≌△CDA;
(2)若AB=![]() ,求阴影部分的面积.
,求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:反比例函数![]() 的图象与一次函数
的图象与一次函数![]() 的图象交于
的图象交于![]() 、
、![]() 两点,其中
两点,其中![]() 点坐标为
点坐标为![]() .
.

(1)求反比例函数与一次函数的表达式;
(2)观察图象,直接写出当![]() 时,自变量
时,自变量![]() 的取值范围;
的取值范围;
(3)一次函数的图象与![]() 轴交于点
轴交于点![]() ,点
,点![]() 是反比例函数图象上的一个动点,若
是反比例函数图象上的一个动点,若![]() ,求此时
,求此时![]() 点的坐标.
点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】工人师傅用一块长为12分米,宽为8分米的矩形铁皮制作一个无盖长方体容器,需要将四角各裁掉一个正方形.(厚度不计)
(1)请在图中画出裁剪示意图,用实线表示裁剪线,虚线表示折痕;并求当长方体底面面积为32平方分米时,裁掉的正方形边长是多少?
(2)若要求制作的长方体的底面长不大于底面宽的5倍(长大于宽),并将容器外表面进行防锈处理,侧面每平方分米的费用为0.5元,底面每平方分米的费用为2元,求裁掉的正方形边长为多少时,总费用最低,最低费用为多少元?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com